题目内容

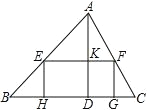
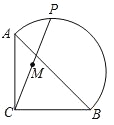
【题目】如图，在等腰 Rt△ABC 中，AC＝BC＝ 2，点 P 在以斜边 AB 为直径的半圆上，M 为 PC的中点．当点 P 沿半圆从点 A 运动至点 B 时，点 M 运动的路径长是（ ）

A. 2 B. 2 C. π D. π

【答案】C

【解析】

取AC的中点D，BC的中点E，连接DE，则点M的运动轨迹是以DE为直径的半圆.证明是等腰直角三角形，再利用勾股定理得出半圆半径，最后利用弧长公式即可求解.

如图所示，取AC的中点D，BC的中点E，连接DE，则点M的运动轨迹是以DE为直径的半圆.在等腰中，AC=BC，，因为D，E分别是AC，BC的中点，所以CD=CE，且，故是等腰直角三角形.在中，由勾股定理得，，故小半圆的半径r=1.根据圆的弧长公式得，点M运动的路径长为.

故本题正确答案为C.

练习册系列答案
相关题目

【题目】如图，抛物线y＝x2+bx﹣c经过直线y＝x﹣3与坐标轴的两个交点A，B，此抛物线与x轴的另一个交点为C，抛物线的顶点为D．

（1）求此抛物线的解析式；

（2）点P为抛物线上的一个动点，求使S△APC：S△ACD＝5：4的点P的坐标．

【题目】图1是一辆吊车的实物图，图2是其工作示意图，AC是可以伸缩的起重臂，其转动点A离地面BD的高度AH为3.4m．当起重臂AC长度为9m，张角∠HAC为118°时，求操作平台C离地面的高度（结果保留小数点后一位：参考数据：sin28°≈0.47，cos28°≈0.88，tan28°≈0.53）

【题目】如图，一次函数y=kx+b与反比例函数y=的图象相交于A（2，3），B（﹣3，n）两点．

（1）求一次函数与反比例函数的解析式；

（2）根据所给条件，请直接写出不等式kx+b＞的解集；

（3）过点B作BC⊥x轴，垂足为C，求S△ABC．

【题目】如图，DC是⊙O的直径，点B在圆上，直线AB交CD延长线于点A，且∠ABD=∠C．

（1）求证：AB是⊙O的切线；

（2）若AB=4cm，AD=2cm，求CD的长．

【题目】如图，锐角△ABC 中，BC＝12，BC 边上的高 AD＝8，矩形 EFGH 的边 GH在 BC 上，其余两点 E、F 分别在 AB、AC 上，且 EF 交 AD 于点 K

(1) 求 的值

(2) 设 EH＝x，矩形 EFGH 的面积为 S

① 求 S 与 x 的函数关系式

② 请直接写出 S 的最大值

【题目】问题原型：如图①，在等腰直角三角形ABC中，∠ACB=90°，BC=a．将边AB绕点B顺时针旋转90°得到线段BD，连结CD．过点D作△BCD的BC边上的高DE， 易证△ABC≌△BDE，从而得到△BCD的面积为．

初步探究：如图②，在Rt△ABC中，∠ACB=90°，BC=a．将边AB绕点B顺时针旋转90°得到线段BD，连结CD．用含a的代数式表示△BCD的面积，并说明理由．

简单应用：如图③，在等腰三角形ABC中，AB=AC，BC=a．将边AB绕点B顺时针旋转90°得到线段BD，连结CD．直接写出△BCD的面积．（用含a的代数式表示）

【题目】如图，四边形ABCD是⊙O的内接四边形，BC的延长线与AD的延长线交于点E，且DC=DE．

（1）求证：∠A=∠AEB；

（2）连接OE，交CD于点F，OE⊥CD，求证：△ABE是等边三角形．

【题目】如图，在平面直角坐标系中，Rt△ABC的三个顶点分别是A（－3，2），B（0，4），C（0，2）．

（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△C；平移△ABC，若A的对应点的坐标为（0，4），画出平移后对应的△；

（2）若将△C绕某一点旋转可以得到△，请直接写出旋转中心的坐标；

（3）在轴上有一点P，使得PA+PB的值最小，请直接写出点P的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网