题目内容
12.商店里某种作业本的零售价为每本2元,为了促销,商店推出两种优惠方案:第一种,购买5本以上,5本按原价,其余按原价的7折优惠;
第二种,购买5本以上,每本按原价的8折优惠.
请问:买10本,买20本作业本分别选哪种方法更优惠?买多少本时,两种优惠方案价格一样?
分析 根据两种优惠方案求得购买10本和20本时的价格;设买x本时两种方案价格相同(x≥5),然后根据优惠价格一样即可列方程求解.
解答 解:买10本时,第一种方案:5×2+(10-5)×2×0.7=17(元),
第二种方案:5×2×0.8=16(元),
则当购买10本时,方案二更优惠;
买20本时,方案一:5×2+(20-5)×0.7=20.5(元),
方案二:20×2×0.8=32(元),
则买20本时,方案一更优惠;
设买x本时两种方案价格相同(x≥5),
根据题意得:5×2+(x-5)×2×0.7=2x×0.8,
解得x=15.
答:当购买数量不超过5本或购买15本时,两种优惠方案价格一样.
点评 本题考查一元一次方程的应用,将现实生活中的事件与数学思想联系起来,读懂题意,列出方程,进行求解.

练习册系列答案
相关题目
10.在 Rt△ABC中,∠C=90°,CD⊥AB,垂足为点D,下列四个三角比正确的是( )
| A. | sinA=$\frac{AC}{AB}$ | B. | cosA=$\frac{AD}{AC}$ | C. | tanA=$\frac{CD}{BD}$ | D. | cotA=$\frac{CD}{AD}$ |
7.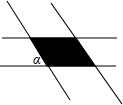 如图,2条宽为1的带子以α角交叉重叠,则重叠部分(阴影部分)的面积为( )
如图,2条宽为1的带子以α角交叉重叠,则重叠部分(阴影部分)的面积为( )
 如图,2条宽为1的带子以α角交叉重叠,则重叠部分(阴影部分)的面积为( )
如图,2条宽为1的带子以α角交叉重叠,则重叠部分(阴影部分)的面积为( )| A. | sinα | B. | $\frac{1}{sinα}$ | C. | $\frac{1}{cosα}$ | D. | $\frac{1}{si{n}^{2}α}$ |
2.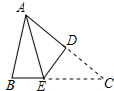 如图,将三角形纸片ABC折叠,使点C与点A重合,折痕为DE.若∠B=80°,∠BAE=26°,则∠EAD的度数为( )
如图,将三角形纸片ABC折叠,使点C与点A重合,折痕为DE.若∠B=80°,∠BAE=26°,则∠EAD的度数为( )
 如图,将三角形纸片ABC折叠,使点C与点A重合,折痕为DE.若∠B=80°,∠BAE=26°,则∠EAD的度数为( )
如图,将三角形纸片ABC折叠,使点C与点A重合,折痕为DE.若∠B=80°,∠BAE=26°,则∠EAD的度数为( )| A. | 36° | B. | 37° | C. | 38° | D. | 45° |
 如图,射线OC平分∠AOB,点P在OC上,且PD⊥OA于点D,PE⊥OB于点E,若OD=8,OP=10,则PE的长为6.
如图,射线OC平分∠AOB,点P在OC上,且PD⊥OA于点D,PE⊥OB于点E,若OD=8,OP=10,则PE的长为6.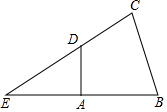 在四边形ABCD中,DA⊥AB.DA=2cm,∠B+∠C=150°.CD与BA的延长线交于E,A刚好是EB中点,P、Q分别是线段CE、BE上的动点,则BP+PQ最小值是(3+2$\sqrt{3}$).
在四边形ABCD中,DA⊥AB.DA=2cm,∠B+∠C=150°.CD与BA的延长线交于E,A刚好是EB中点,P、Q分别是线段CE、BE上的动点,则BP+PQ最小值是(3+2$\sqrt{3}$).