题目内容
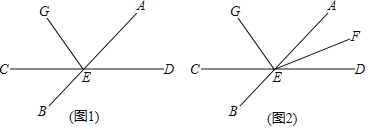
【题目】如图,直线AB与CD相交于点E,射线EG在∠AEC内(如图1).
(1)若∠BEC的补角是它的余角的3倍,则∠BEC= °;
(2)在(1)的条件下,若∠CEG比∠AEG小25度,求∠AEG的大小;
(3)若射线EF平分∠AED,∠FEG=m°(m>90°)(如图2),则∠AEG﹣∠CEG= °(用m的代表式表示).
【答案】(1)45°;(2)∠AEG=80°;(3)2m﹣180
【解析】
(1)设∠BEC=x°,根据题意,可列方程:180﹣x=3(90﹣x),解出∠BEC;
(2)由∠CEG=∠AEG﹣25°,得∠AEG=180°﹣∠BEC﹣∠CEG=180°﹣45°﹣(∠AEG﹣25°),解出∠AEG;
(3)计算出∠AEG和∠CEG,然后相减,即可得到结果.
解:(1)设∠BEC=x°,
根据题意,可列方程:180﹣x=3(90﹣x),
解得x=45°,
故∠BEC=45°,
故答案为:45°;
(2)∵∠CEG=∠AEG﹣25°,
∴∠AEG=180°﹣∠BEC﹣∠CEG
=180°﹣45°﹣(∠AEG﹣25°)=160°﹣∠AEG,
∴∠AEG=80°;
(3)∵EF平分∠AED,
∴∠AEF=∠DEF,
设∠AEF=∠DEF=α,∠AEG=∠FEG﹣∠AEF=m﹣α,
∠CEG=180°﹣∠GEF﹣DEF=180﹣m﹣α,
∴∠AEG﹣∠CEG=m﹣α﹣(180﹣m﹣α)=2m﹣180.
故答案为:2m﹣180.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目