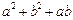题目内容
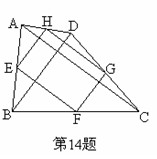
如图,四边形ABCD中,对角线AC⊥BD,E、F、G、H分别是各边的中点,若AC = 4cm,BD = 6cm,则四边形EFGH的面积是 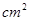
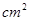

6
根据E、F、G、H分别是各边的中点,利用三角形中位线定理求出EH和EF,判定四边形EFGH是矩形,然后即可四边形EFGH的面积.
解;∵E、F、G、H分别是四边形ABCD各边的中点,
∴EH∥BD且EH=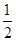 BD,FG∥BD且=
BD,FG∥BD且=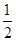 BD,
BD,
∴EH∥FG,EH=FG,
同理EF∥HG,EF=HG,
又∵AC⊥BD,
∴四边形ABCD是矩形,
∴四边形ABCD=EF×EH=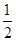 AC×
AC×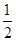 BD=
BD=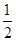 ×4×
×4×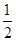 ×6=6cm2.
×6=6cm2.
解;∵E、F、G、H分别是四边形ABCD各边的中点,
∴EH∥BD且EH=
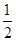 BD,FG∥BD且=
BD,FG∥BD且=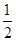 BD,
BD,∴EH∥FG,EH=FG,
同理EF∥HG,EF=HG,
又∵AC⊥BD,
∴四边形ABCD是矩形,
∴四边形ABCD=EF×EH=
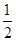 AC×
AC×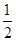 BD=
BD=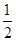 ×4×
×4×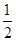 ×6=6cm2.
×6=6cm2.
练习册系列答案
相关题目
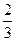 ,BF=3米,BC=1米,CD=6米.求:
,BF=3米,BC=1米,CD=6米.求: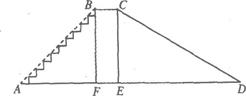
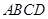 ,有以下四个条件:①
,有以下四个条件:①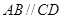 ;②
;②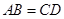 ;③
;③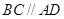 ;④
;④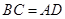 .从这四个条件中任选两个,能使四边形
.从这四个条件中任选两个,能使四边形 中,
中,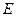 是
是 边上一点,
边上一点, 为
为 延长线上的点,
延长线上的点, .
.
 ≌△
≌△
 ,求
,求 的度数
的度数
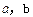 的矩形,它的周长为14,面积为10,求下列各式的值:(1)
的矩形,它的周长为14,面积为10,求下列各式的值:(1)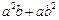 (2)
(2)