题目内容
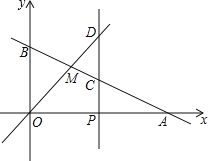
【题目】如图,已知函数y=﹣![]() x+3的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M.
x+3的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M.
(1)分别求出点A、点M的坐标;
(2)在x轴上有一动点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣![]() x+3和y=x的图象于点C、D,且OB=2CD,求a的值.
x+3和y=x的图象于点C、D,且OB=2CD,求a的值.
【答案】详见解析
【解析】
试题分析:(1)将y=0代入y=﹣![]() x+3,求出x的值,得到A点坐标;解方程组
x+3,求出x的值,得到A点坐标;解方程组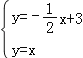 ,求出点M的坐标;
,求出点M的坐标;
(2)先确定B点坐标为(0,3),则OB=2CD=3,再表示出C点坐标为(a,﹣![]() a+3),D点坐标为(a,a),所以a﹣(﹣
a+3),D点坐标为(a,a),所以a﹣(﹣![]() a+3)=
a+3)=![]() ,然后解方程即可.
,然后解方程即可.
解:(1)在函数y=﹣![]() x+3中,
x+3中,
令y=0,得﹣![]() x+3=0,解得x=6,
x+3=0,解得x=6,
则点A的坐标为(6,0).
由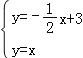 ,解得
,解得![]() ,
,
则点M的坐标为(2,2);
(2)由题意得:C(a,﹣![]() a+3),D(a,a),
a+3),D(a,a),
∴CD=a﹣(﹣![]() a+3).
a+3).
∵OB=2CD=3,
∴a﹣(﹣![]() a+3)=
a+3)=![]() ,
,
∴a=3.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目