题目内容
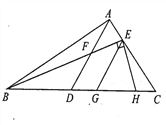
【题目】如图，在△ABC中，点D在BC 上，点E 在AC 上，AD交BE于F. 已知EG∥AD交BC于G, EH⊥BE交BC于H，∠HEG = 50°.
（1）求∠BFD的度数.
（2）若∠BAD = ∠EBC，∠C = 41°，求∠BAC的度数.
【答案】（1）∠BFD=40°（2）∠BAC=99°
【解析】（1）根据垂直的定义可得∠BEH=90°，然后求出∠BEG=40°，再根据两直线平行线，同位角相等可得∠BFD=∠BEG；
（2）根据三角形的一个外角等于与它不相邻的两个内角的和可得∠BFD=∠EBC+∠ABE=∠ABC，然后根据三角形的内角和定理列式计算即可得解．
试题解析：（1）∵EH⊥BE，
∴∠BEH=90°，
∵∠HEG=50°，
∴∠BEG=40°，
又∵EG∥AD，
∴∠BFD=∠BEG=40°；
（2）∵∠BFD=∠BAD+∠ABE，∠BAD=∠EBC，
∴∠BFD=∠EBC+∠ABE=∠ABC=40°，
∵∠C=41°，
∴∠BAC=180°-∠ABC-∠C=180°-40°-41°=99°．
练习册系列答案
开心蛙状元作业系列答案
课时掌控随堂练习系列答案
一课一练一本通系列答案
相关题目
