题目内容
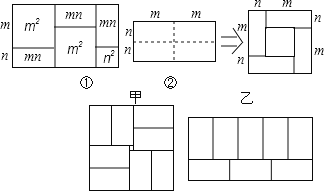
【题目】有许多代数恒等式可以用图形的面积来表示,如图①,它表示了(2m+n)(m+n)=2m2+3mn+n2.
(1)图②是将一个长2m、宽2n的长方形,沿图中虚线平方为四块小长方形,然后再拼成一个正方形,请你观察图形,写出三个代数式(m+n)2、(m-n)2、mn关系的等式: ;
(2)若已知x+y=7、xy=10,则(x-y) 2= ;
(3)小明用8个一样大的长方形(长acm,宽bcm)拼图,拼出了如图甲、乙的两种图案,图案甲是一个正方形,图案乙是一个大的长方形,图案甲的中间留下了边长是2cm的正方形小洞,则(a+2b)2-8ab的值为 .
【答案】(1)![]() ;(2)9;(3)4.
;(2)9;(3)4.
【解析】试题分析:(1)利用图形面积关系得出等式即可;
(2)利用图形面积之间关系得出(x﹣y)2=(x+y)2﹣4xy即可求出;
(3)利用图形面积之间关系得出(a+2b)2﹣8ab=(a﹣2b)2即可求出.
试题解析:解:(1)由图形的面积可得出:
(m+n)2=(m﹣n)2+4mn;
故答案为:(m+n)2=(m﹣n)2+4mn;
(2)∵x+y=7、xy=10,则(x﹣y)2=(x+y)2﹣4xy=72﹣4×10=9.
故答案为:9;
(3)∵(a+2b)2﹣8ab=(a﹣2b)2=22=4(cm2),∴(a+2b)2﹣8ab的值为4cm2.
故答案为:4cm2.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目