题目内容
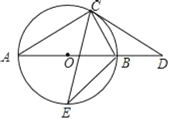
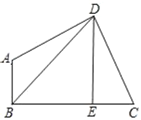
【题目】已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,DE⊥BC于E,连接BD,设AD=m,DC=n,BE=p,DE=q.
(1)若tanC=2,BE=3,CE=2,求点B到CD的距离;
(2)若m=n, BD=3![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
【答案】(1)![]() ;(2)9.
;(2)9.
【解析】
(1)要求点B到CD的距离,于是作垂线构造直角三角形,又知tanC=2,BE=3,CE=2,可以得到BF=2FC,设未知数根据勾股定理列方程可以求解;
(2)m=n,即AD=DC,通过作垂线,构造全等三角形将问题转化为求正方形BEDG的面积即可.
(1)过点B作BF⊥CD,垂足为F,则∠BFC=90°,
∵DE⊥BC,
∴∠DEC=∠DEB=90°,
在Rt△DEC中,∵tanC=2,EC=2,
∴DE=4,
在Rt△BFC中,∵tanC=2,∴BF=2FC,
设BF=x,则FC=![]() x,∵BF2+FC2=BC2,
x,∵BF2+FC2=BC2,
∴x2+(![]() x)2=(3+2)2,
x)2=(3+2)2,
解得:x=![]() ,即:BF=
,即:BF=![]() ,
,
答:点B到CD的距离是![]() ;
;
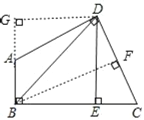
(2)过点D作DG⊥AB,交BA的延长线相交于点G,
∵四边形ABCD的内角和是360°,∠ABC=∠ADC=90°,
∴∠C+∠BAD=180°,
又∵∠BAD+∠GAD=180°,
∴∠C=∠GAD,
∵∠DEC=∠G=90°,AD=CD
∴△DEC≌△DGA,(AAS)
∴DE=DG,
∴四边形BEDG是正方形,
∴S四边形ABCD=S正方形BEDG=![]() BD2=9.
BD2=9.
答:四边形ABCD的面积是9.

 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案【题目】阅读下列材料:
材料一:
早在2011年9月25日,北京故宫博物院就开始尝试网络预售门票,2011年全年网络售票仅占1.68%.2012年至2014年,全年网络售票占比都在2%左右.2015年全年网络售票占17.33%,2016年全年网络售票占比增长至41.14%.2017年8月实现网络售票占比77%.2017年10月2日,首次实现全部网上售票.与此同时,网络购票也采用了“人性化”的服务方式,为没有线上支付能力的观众提供代客下单服务.实现全网络售票措施后,在北京故宫博物院的精细化管理下,观众可以更自主地安排自己的行程计划,获得更美好的文化空间和参观体验.
材料二:
以下是某同学根据网上搜集的数据制作的2013-2017年度中国国家博物馆参观人数及年增长率统计表.
年度 | 2013 | 2014 | 2015 | 2016 | 2017 |
参观人数(人次) | 7 450 000 | 7 630 000 | 7 290 000 | 7 550 000 | 8 060 000 |
年增长率(%) | 38.7 | 2.4 | -4.5 | 3.6 | 6.8 |

他还注意到了如下的一则新闻:2018年3月8日,中国国家博物馆官方微博发文,宣布取消纸质门票,观众持身份证预约即可参观. 国博正在建设智慧国家博物馆,同时馆方工作人员担心的是:“虽然有故宫免(纸质)票的经验在前,但对于国博来说这项工作仍有新的挑战.参观故宫需要观众网上付费购买门票,他遵守预约的程度是不一样的.但(国博)免费就有可能约了不来,挤占资源,所以难度其实不一样.” 尽管如此,国博仍将积极采取技术和服务升级,希望带给观众一个更完美的体验方式.
根据以上信息解决下列问题:
(1)补全以下两个统计图;
(2)请你预估2018年中国国家博物馆的参观人数,并说明你的预估理由.