题目内容
【题目】某商店准备购进甲、乙两种商品.已知甲商品每件进价15元,售价20元;乙商品每件进价35元,售价45元.
(1)若该商店同时购进甲、乙两种商品共100件,恰好用去2700元,求购进甲、乙两种商品各多少件?
(2)若该商店准备用不超过3100元购进甲、乙两种商品共100件,且这两种商品全部售出后获利不少于890元,问应该怎样进货,才能使总利润最大,最大利润是多少?(利润=售价﹣进价)
【答案】(1) 商店购进甲种商品40件,购进乙种商品60件;(2) 应购进甲种商品20件,乙种商品80件,才能使总利润最大,最大利润为900元.
【解析】
(1)设购进甲、乙两种商品分别为x件与y件,根据甲种商品件数+乙种商品件数=100,甲商品的总进价+乙种商品的总进价=2700,列出关于x与y的方程组,求出方程组的解即可得到x与y的值,得到购进甲、乙两种商品的件数;
(2)设商店购进甲种商品a件,则购进乙种商品(100-a)件,根据甲商品的总进价+乙种商品的总进价小于等于3100,甲商品的总利润+乙商品的总利润大于等于890列出关于a的不等式组,求出不等式组的解集,得到a的取值范围,根据a为正整数得出a的值,再表示总利润W,发现W与a成一次函数关系式,且为减函数,故a取最小值时,W最大,即可求出所求的进货方案与最大利润.
(1)设购进甲种商品x件,购进乙商品y件,
根据题意得:
![]() ,
,
解得:![]() ,
,
答:商店购进甲种商品40件,购进乙种商品60件;
(2)设商店购进甲种商品a件,则购进乙种商品(100﹣a)件,
根据题意列得:
![]() ,
,
解得:20≤a≤22,
∵总利润W=5a+10(100﹣a)=﹣5a+1000,W是关于a的一次函数,W随a的增大而减小,
∴当a=20时,W有最大值,此时W=900,且100﹣20=80,
答:应购进甲种商品20件,乙种商品80件,才能使总利润最大,最大利润为900元.

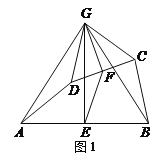
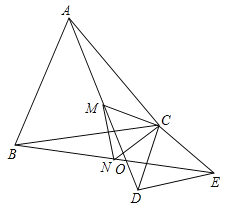
【题目】已知:如图,![]() 、
、![]() 都是等腰三角形,且
都是等腰三角形,且![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 相交于点
相交于点![]() ,点
,点![]() 、
、![]() 分别是线段
分别是线段![]() 、
、![]() 的中点.以下4个结论:①
的中点.以下4个结论:①![]() ;②
;②![]() ;③
;③![]() 是等边三角形;④连
是等边三角形;④连![]() ,则
,则![]() 平分
平分![]() 以上四个结论中正确的是:______.(把所有正确结论的序号都填上)
以上四个结论中正确的是:______.(把所有正确结论的序号都填上)
【题目】某市扶贫办在精准扶贫工作中,组织30辆汽车装运花椒、核桃、甘蓝向外地销售.按计划30辆车都要装运,每辆汽车只能装运同一种产品,且必须装满,根据下表提供的信息,解答以下问题:
产品名称 | 核桃 | 花椒 | 甘蓝 |
每辆汽车运载量(吨) | 10 | 6 | 4 |
每吨土特产利润(万元) | 0.7 | 0.8 | 0.5 |
若装运核桃的汽车为x辆,装运甘蓝的车辆数是装运核桃车辆数的2倍多1,假设30辆车装运的三种产品的总利润为y万元.
(1)求y与x之间的函数关系式;
(2)若装花椒的汽车不超过8辆,求总利润最大时,装运各种产品的车辆数及总利润最大值.
【题目】今年是“五四”运动![]() 周年,为进一步弘扬“爱国、进步、民主、科学”的五四精神,引领广大团员青年坚定理想信念,某市团委、少先队共同举办纪念“五四运动
周年,为进一步弘扬“爱国、进步、民主、科学”的五四精神,引领广大团员青年坚定理想信念,某市团委、少先队共同举办纪念“五四运动![]() 周年”读书演讲比赛,甲同学代表学校参加演讲比赛,
周年”读书演讲比赛,甲同学代表学校参加演讲比赛,![]() 位评委给该同学的打分(单位:分)情况如下表:
位评委给该同学的打分(单位:分)情况如下表:
评委 | 评委1 | 评委2 | 评委3 | 评委4 | 评委5 | 评委6 | 评委7 |
打分 |
|
|
|
|
|
|
|
(1)直接写出该同学所得分数的众数与中位数;
(2)计算该同学所得分数的平均数.