Question

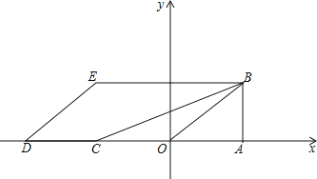
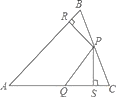
【题目】如图在△ABC中，P、Q分别是BC、AC上的点，作PR⊥AB，PS⊥AC，垂足分别是R、S，若AQ=PQ，PR=PS,AB=AC，下面三个结论：①AS=AR；②PQ∥AB；③△BRP≌△CSP，其中正确的是（　　）

A. ①② B. ②③ C. ①③ D. ①②③

Answer 1

【答案】D

【解析】连接AP

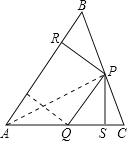
在Rt△ASP和Rt△ARP中

PR=PS，PA=PA

所以Rt△ASP≌Rt△ARP

所以①AS=AR正确

因为AQ=PQ

所以∠QAP=∠QPA

又因为Rt△ASP≌Rt△ARP

所以∠PAR=∠PAQ

于是∠RAP=∠QPA

所以②PQ∥AR正确

③由AB=AC，AS=AR得BR=CS,又PR=PS，∠BRP=∠CSP, ∴△BRP≌△CSP，根据现有条件无法确定其全等。

故填①②③。

故选：D