��Ŀ����
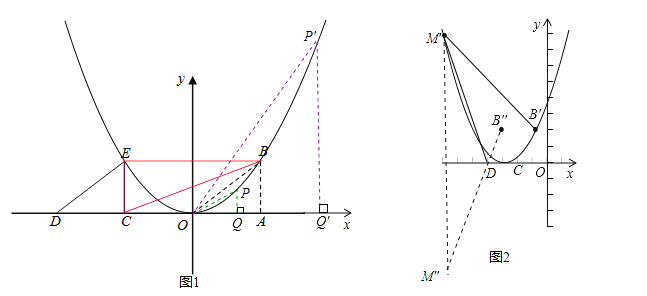
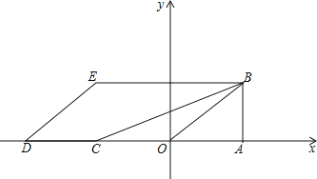
����Ŀ����ͼ������OAB������ƽ��ֱ������ϵxOy�У���OAB=90����OA=2��AB=![]() ������OAB��x��ĸ�����ƽ��2OA�ij��Ⱥ�õ���DCE��
������OAB��x��ĸ�����ƽ��2OA�ij��Ⱥ�õ���DCE��
��1������ԭ���������y=ax2+bx+c������B��E����������ߵĽ���ʽ��
��2������P�ڸ����������ƶ�������p�ڵ�һ������ʱ������p��PQ��x���ڵ�Q������OP������O��P��QΪ���������������B��C��EΪ��������������ƣ�ֱ��д����P�����ꣻ
��3������M����4��n���ڸ��������ϣ�ƽ�������ߣ���ƽ�ƺ��M�Ķ�Ӧ��ΪM������B�Ķ�Ӧ��ΪB���������������������ƽ��ʱ���Ƿ����ij��λ�ã�ʹ�ı���M��B��CD���ܳ���̣������ڣ������ʱ�����ߵĽ���ʽ���������ڣ���˵�����ɣ�
���𰸡���1��y=![]() x2����2��P��1��
x2����2��P��1��![]() ����P ��
����P ��![]() ��
��![]() ������3�����ڣ�������������ƽ��
������3�����ڣ�������������ƽ��![]() ����λʱ���ı���M��B��CD���ܳ���̣���ʱ�����ߵĽ���ʽΪy=
����λʱ���ı���M��B��CD���ܳ���̣���ʱ�����ߵĽ���ʽΪy=![]() ��x+
��x+![]() ��2��
��2��
��������
�����������1������ƽ�Ƶ��������B��E�����꣬Ȼ�����ô���ϵ����������ú����Ľ���ʽ����2����P���������Ϊ��x��![]() ������Ϊ��BEC=��OQP=90����������O��P��QΪ���������������B��C��EΪ���������������ʱ��Q��Eһ����Ӧ��Ȼ�����������������ۣ���i����OQP�ס�BEC����ii����PQO�ס�BEC���������������ζ�Ӧ�߳ɱ����г�����ʽ����⼴�ɣ���3������ƽ��ʱ��ʹM'D+CB'��̼��ɣ���ô������M������x��ԳƵ������ΪM�����õ�ֱ��B��M���Ľ���ʽ����y=0�������Ӧ�ĵ�����ꣻ�����õ������߶���ƽ�ƵĹ��ɣ��ö���ʽ�����Ӧ�ĺ�������ʽ�����¶���������뼴��.
������Ϊ��BEC=��OQP=90����������O��P��QΪ���������������B��C��EΪ���������������ʱ��Q��Eһ����Ӧ��Ȼ�����������������ۣ���i����OQP�ס�BEC����ii����PQO�ס�BEC���������������ζ�Ӧ�߳ɱ����г�����ʽ����⼴�ɣ���3������ƽ��ʱ��ʹM'D+CB'��̼��ɣ���ô������M������x��ԳƵ������ΪM�����õ�ֱ��B��M���Ľ���ʽ����y=0�������Ӧ�ĵ�����ꣻ�����õ������߶���ƽ�ƵĹ��ɣ��ö���ʽ�����Ӧ�ĺ�������ʽ�����¶���������뼴��.
�����������1��������ã�B��2��![]() ������OC=2��CE=
������OC=2��CE=![]() ����E����2��
����E����2��![]() ����
����
�������߾���ԭ��͵�B��E�����������ߵĽ���ʽΪy=ax2��a��0����
�������߾�����B��2��![]() ������
������![]() =4a����ã�a=
=4a����ã�a=![]() ��
��
�������ߵĽ���ʽΪy=![]() x2��
x2��
��2������P���������ϣ������P������Ϊ��x��![]() x2����
x2����
�������������i������OQP�ס�BECʱ����![]() ����
���� 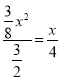 ����ã�x=1������P������Ϊ��1��
����ã�x=1������P������Ϊ��1��![]() ����
����
��ii������PQO�ס�BECʱ����![]() ����
����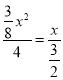 ����ã�x=
����ã�x=![]() ������P������Ϊ��
������P��������![]() ��
��![]() ����
����
�������������������ĵ�P��������P��1��![]() ����P ��
����P ��![]() ��
��![]() ����
����
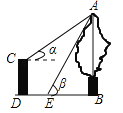
��3�����ڣ�
��Ϊ�߶�M��B����CD�ij��Ƕ�ֵ������Ҫʹ�ı���M��B��CD���ܳ���̣�ֻҪʹM��D+CB����̣�
���������������ƽ�ƣ���Ȼ��M��D+CB����MD+CB����˲�����ij��λ�ã�ʹ�ı���M��B��CD���ܳ���̣���ȻӦ�ý������� y=![]() x2����ƽ�ƣ�
x2����ƽ�ƣ�
����֪M����4��6����������������ƽ����n����λ�����M����B��������ֱ�Ϊ
M������4��n��6����B����2��n��![]() ����
����
��ΪCD=2����˽���B������ƽ��2����λ��B������n��![]() ����
����
ҪʹM��D+CB����̣�ֻҪʹM��D+DB����̣���M������x��ԳƵ������ΪM������4��n����6����
��ֱ��M��B���Ľ���ʽy=kx+b��k��0������DӦ��ֱ��M��B���ϣ�
��ֱ��M��B���Ľ���ʽΪy=![]() ����B������n��
����B������n��![]() �����룬���n=
�����룬���n=![]() ��
��
�ʽ�����������ƽ��![]() ����λʱ���ı���M��B��CD���ܳ���̣���ʱ�����ߵĽ���ʽΪy=
����λʱ���ı���M��B��CD���ܳ���̣���ʱ�����ߵĽ���ʽΪy=![]() ��x+
��x+![]() ��2��
��2��