题目内容
⊙O的半径为5cm，AB为直径，CD为弦，CD⊥AB，垂足为E，若CD=6cm，则AE=________cm．
1或9
分析：连接OC，在Rt△OCE中，由于直径AB⊥CD，由垂径定理可得到直角边CE的长，已知了圆的半径，即可由勾股定理求得OE的长，那么AE的长即为OA+OE或OA-OE，由此得解．
解答：
解：连接OC；
∵AB是⊙O的直径，且AB⊥CD，
∴CE=DE=3cm；
在Rt△OCE中，OC=5cm，CE=3cm，由勾股定理得：
OE=
=4cm；
∴AE=OE+OA=9cm或AE=OA-OE=1cm．
故AE的长为1或9cm．
点评：此题主要考查了垂径定理和勾股定理的综合应用，需要注意的是AE的长有两种情况，不要漏解．
分析：连接OC，在Rt△OCE中，由于直径AB⊥CD，由垂径定理可得到直角边CE的长，已知了圆的半径，即可由勾股定理求得OE的长，那么AE的长即为OA+OE或OA-OE，由此得解．
解答：
解：连接OC；∵AB是⊙O的直径，且AB⊥CD，
∴CE=DE=3cm；
在Rt△OCE中，OC=5cm，CE=3cm，由勾股定理得：
OE=
=4cm；∴AE=OE+OA=9cm或AE=OA-OE=1cm．
故AE的长为1或9cm．
点评：此题主要考查了垂径定理和勾股定理的综合应用，需要注意的是AE的长有两种情况，不要漏解．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
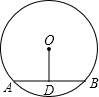如图，⊙O的半径为5cm，圆心O到弦AB的距离OD为3cm，则弦AB的长为