题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,D是AB边上一点,以BD为直径的⊙O与边AC相切于点E,连结DE并延长,与BC的延长线交于点F. 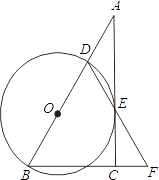
(1)求证:BD=BF;
(2)若BC=6,AD=4,求sinA的值.
【答案】
(1)证明:连结OE.
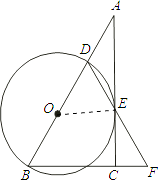
∵AC切⊙O于E,
∴OE⊥AC,
又∵∠ACB=90°即BC⊥AC,
∴OE∥BC
∴∠OED=∠F.
又∵OD=OE,
∴∠OED=∠ODE,
∴∠ODE=∠F
∴BD=BF
(2)解:设⊙O半径为r,由(1)知,OE∥BC得△AOE∽△ABC.
∴ ![]() ,即
,即 ![]() ,
,
∴r2﹣r﹣12=0,
解之得r1=4,r2=﹣3(舍去).
在Rt△AOE中,
∴sinA= ![]()
【解析】(1)利用三角形中位线定理证得OE∥BC.所以由平行线的性质、等腰三角形的性质推知∠ODE=∠F,则易证得结论;(2)设⊙O半径为r.根据相似三角形△AOE∽△ABC的对应边成比例列出关于半径r的方程,通过解方程即可求得r的值.然后通过解Rt△AOE来求sinA的值.
【考点精析】关于本题考查的切线的性质定理和相似三角形的判定与性质,需要了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能得出正确答案.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目