题目内容
【题目】如图,矩形ABCD中,AD=2AB,E、F、G、H分别是AB,BC,CD,AD边上的点,EG⊥FH,FH=2 ![]() ,则四边形EFGH的面积为( )
,则四边形EFGH的面积为( ) 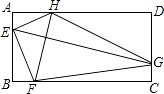
A.8 ![]()
B.8
C.12 ![]()
D.24
【答案】B
【解析】解:过F作FM⊥AD于M,过E作EN⊥CD于N,EN与MF交于点Z, 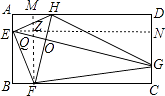
则∠FMH=∠ENG=90°,
∵四边形ABCD是矩形,EG⊥FH,
∴∠A=∠D=∠AEN=∠EOF=∠EZF=90°,
∴四边形AEND是矩形,
∴AD=EN,
同理AB=FM,
∵AD=2AB,
∴EN=2FM,
∵∠NEG+∠EQZ+∠EZQ=180°,∠MFH+∠EOF+∠FQO=180°,∠EQZ=∠FQO,
∴∠MFH=∠NEG,
∵∠FMH=∠ENG=90°,
∴△FMH∽△ENG,
∴ ![]() =2,
=2,
∵FH=2 ![]() ,
,
∴EG=4 ![]() ,
,
∴ ![]() EGπEG×FH=
EGπEG×FH= ![]() ×2
×2 ![]() ×4
×4 ![]() =8,
=8,
故选:B.
过F作FM⊥AD于M,过E作EN⊥CD于N,根据矩形的性质和判定推出EN=2FH,求出EN的长,即可得出答案.

练习册系列答案
相关题目