题目内容
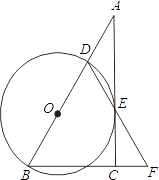
【题目】将△ABC的边AB绕点A顺时针旋转α得到AB′,边AC绕点A逆时针旋转β得到AC′,α+β=180°.连接B′C′,作△AB′C′的中线AD.
(初步感知)
(1)如图①,当∠BAC=90°,BC=4时,AD的长为______;
(探索证明)
(2)如图②,△ABC为任意三角形时,猜想AD与BC的数量关系,并证明;
(应用延伸)
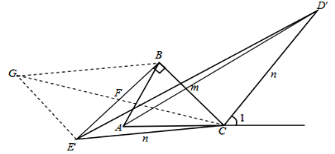
(3)如图③,已知等腰△ACB,AC=BC=m,延长AC到D,延长CB到E,使CD=CE=n,将△CED绕C顺时针旋转一周得到△CE′D′,连接BE′、AD′,若∠CBE′=90°,求AD′的长度(用含m、n的代数式表示).



【答案】(1)2;(2)(2)AD=![]() BC,理由见解析;(3)AD′=
BC,理由见解析;(3)AD′=![]() .
.
【解析】(1)首先证明△BAC≌△B′AC′,根据直角三角形斜边中线定理即可解决问题;
(2)结论:AD=![]() BC.如图,延长AD到E,使得DE=AD,连接B′E,C′E,首先证明四边形AC′EB′是平行四边形,再证明△BAC≌△AB′E,即可解决问题;
BC.如图,延长AD到E,使得DE=AD,连接B′E,C′E,首先证明四边形AC′EB′是平行四边形,再证明△BAC≌△AB′E,即可解决问题;
(3)分情况进行讨论即可得.
(1)∵∠BAC=90°,∠BAC+∠B′AC′=180°,
∴∠B′AC′=∠BAC=90°,
∵AB=AB′,AC=AC′,
∴△BAC≌△B′AC′,
∴BC=B′C′,
∵B′D=DC′,
∴AD=![]() B′C′=
B′C′=![]() BC=
BC=![]() =2,
=2,
故答案为:2;
(2)AD=![]() BC,理由如下:
BC,理由如下:
如图,延长AD至点E,使得DE=AD,
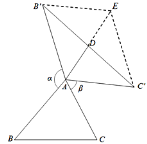
∵B′D=C′D,∴四边形AC′EB′为平行四边形,
∴B′E∥AC′,B′E=AC′=AC,∴∠AB′E+∠B′AC′=180°,
∵α+β=180°,∴∠BAC+∠B′AC′=180°,∴∠AB′E=∠BAC,
∵AB′=AB,∴△AB′E≌△BAC,∴AE=BC,
∴AD=![]() AE=
AE=![]() BC;
BC;
(3)情况一:如图,过点C作△BCE′的中线CF,
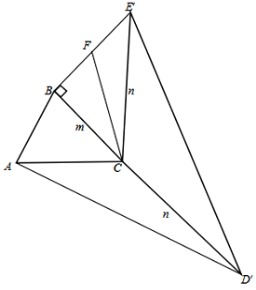
在Rt△BCE′中,由勾股定理
得:![]() ;
;
∴BF=![]() BE′=
BE′=![]() ,
,
在Rt△BCF中,由勾股定理得:CF=![]() =
=![]() =
=![]() ,
,
由(2)可知:AD′=![]() ;
;
情况二:如图,作△CBE′的中线CF并延长到G,使FG=CF,连接BG、E′G,
∵BF=E′F,CF=GF,∴四边形BCE′G为平行四边形,
∴BC=GE′,BC∥GE′,∵BC=AC,∴AC=GE′,
由旋转可知∠1=∠BCE′,∵∠1+∠ACD′=180°,∠GE′C+∠BCE′=180°,∴∠ACD′=∠GE′C,
∵CD′=E′C,∴△ACD′≌△GE′C,∴AD′=GC
由情况一可知:BE′=![]() ,AD′=
,AD′=![]() .
.