题目内容
如图,已知△ABC中,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E,连接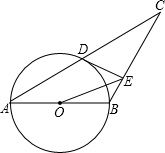 OE,CD=
OE,CD=| 3 |
(1)求证:DE是⊙O的切线;
(2)分别求AB,OE的长;
(3)填空:如果以点E为圆心,r为半径的圆上总存在不同的两点到点O的距离为1,则r的取值范围为
分析:(1)要证明DE是⊙O的切线,已知OD是圆的半径,只要证明OD⊥DE即可.
(2)根据勾股定理可求得BC的长,从而可求得AB,DE的长,再根据勾股定理即可求得OE的长.
(3)由第二问可知OE的长,根据题意不难求得圆E的半径r的取值范围.
(2)根据勾股定理可求得BC的长,从而可求得AB,DE的长,再根据勾股定理即可求得OE的长.
(3)由第二问可知OE的长,根据题意不难求得圆E的半径r的取值范围.
解答: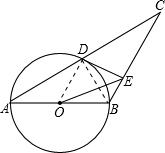 (1)证明:连接BD、OD,
(1)证明:连接BD、OD,
∵AB是直径,
∴∠ADB=90°,
又∵AB=BC,
∴AD=CD.
∵AO=BO,
∴OD是△ABC的中位线,
 ∴OD∥BC.
∴OD∥BC.
∵DE⊥BC,
∴OD⊥DE,
∴DE是⊙O的切线.
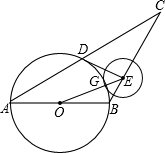
(2)解:在Rt△CBD中,CD=
,∠ACB=30°
∴BC=
=2,
∴BD=1,AB=2,
 在Rt△CDE中,CD=
在Rt△CDE中,CD=
,∠ACB=30°
∴DE=
CD=
,BC=
=2
∵OD是圆O半径,
∴OD=1,
∴OE=
=
.
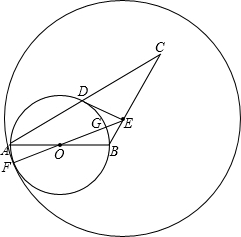
(3)解:如图,
当圆E的半径为
-1时,OG=1;
当圆E的半径为
+1时,OG=1,
故
-1<r<
+1.
 (1)证明:连接BD、OD,
(1)证明:连接BD、OD,∵AB是直径,
∴∠ADB=90°,
又∵AB=BC,
∴AD=CD.
∵AO=BO,
∴OD是△ABC的中位线,
 ∴OD∥BC.
∴OD∥BC.∵DE⊥BC,
∴OD⊥DE,
∴DE是⊙O的切线.
(2)解:在Rt△CBD中,CD=
| 3 |
∴BC=
| CD |
| cos30° |
∴BD=1,AB=2,
 在Rt△CDE中,CD=
在Rt△CDE中,CD=| 3 |
∴DE=
| 1 |
| 2 |
| ||
| 2 |
| CD |
| cos30° |
∵OD是圆O半径,
∴OD=1,
∴OE=
| OD2+DE2 |
| ||
| 2 |
(3)解:如图,
当圆E的半径为
| ||
| 2 |
当圆E的半径为
| ||
| 2 |
故
| ||
| 2 |
| ||
| 2 |
点评:此题主要考查学生对切线的判定及勾股定理等知识点的综合运用能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF.
如图,已知△ABC中,AB=AC,E、F分别在AB、AC上且AE=CF. 如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( )
如图,已知△ABC中,P是AB上一点,连接CP,以下条件不能判定△ACP∽△ABC的是( ) (2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( )
(2012•梓潼县一模)如图,已知△ABC中,∠C=90°,AC=4,BC=3,则sinA=( ) 如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( )
如图,已知△ABC中,BC=8,BC边上的高h=4,D为BC上一点,EF∥BC交AB于E,交AC于F(EF不过A、B),设E到BC的距离为x,△DEF的面积为y,那么y关于x的函数图象大致是( ) 如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )
如图,已知△ABC中,AB=AC,D是BC中点,则下列结论不正确的是( )