题目内容
【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=116°,∠ACF=25°,求∠FEC的度数. 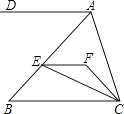
【答案】解:∵EF∥AD,AD∥BC, ∴EF∥BC,
∴∠ACB+∠DAC=180°,
∵∠DAC=116°,
∴∠ACB=64°,
又∵∠ACF=25°,
∴∠FCB=∠ACB﹣∠ACF=39°,
∵CE平分∠BCF,
∴∠BCE=19.5°,
∵EF∥BC,
∴∠FEC=∠ECB,
∴∠FEC=19.5°
【解析】由EF与AD平行,AD与BC平行,利用平行于同一条直线的两直线平行得到EF与BC平行,利用两直线平行同旁内角互补求出∠ACB度数,进而求出∠FCB度数,根据CE为角平分线求出∠BCE度数,再利用两直线平行内错角相等即可求出所求角度数.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目