Question

【题目】如图，已知AB是⊙O的直径，BC是⊙O的切线，B为切点，OC平行于弦AD，连接CD。过点D作DE⊥AB于E，交AC于点P，求证：点P平分线段DE。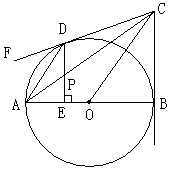

Answer 1

【答案】证明：连结OD ， OD∥AD ，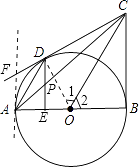

∴∠1＝∠ADO ， ∠2＝∠DAO ，
∵OA=OD ， ∴∠ADO=∠DAO ，
∴∠1＝∠2，∵OD＝OB，OC＝OC，
∴△ODC≌△OBC ， ∴∠ODC＝∠OBC。
∵OB是⊙O的半径，BC是⊙O的切线，
∴BC⊥OB
∴∠OBC＝900 ， ∴∠ODC＝900 ， ∴CD⊥OD。
∴CD是⊙O的切线。
过A作⊙O的切线AF ， 交CD的延长线于点F ， 则FA⊥AB。
∵DE⊥AB ， CB⊥AB ， ∴FA∥DE∥CB,
∴ 。
在△FAC中，∵DP∥FA, ∴ 。
∵FA、FD是⊙O的切线，∴FA=FD，∴ 。
在△ABC中，∵EP∥BC, ∴ 。
∵CD、CB是⊙O的切线，∴CB=CD ， ，
∴ ， ∴DP=EP ，
∴点P平分线段DE.
【解析】出现切线时，连接圆心和切点，过A作平行线，可由DP∥FA得到 ,可由EP∥BC得到,再利用切线长定理得出CB=CD,进而证出DP=EP.