题目内容
【题目】如图△ABC内接于圆O,I是△ABC的内心,AI的延长线交圆O于点D.
(1)求证:BD=DI;
(2)若OI⊥AD,求![]() 的值.
的值.
【答案】(1)证明:∵点I是△ABC的内心
∴∠BAD=∠CAD,∠ABI=∠CBI
∵∠CBD=∠CAD
∴∠BAD=∠CBD
∴∠BID=∠ABI+∠BAD,∠BAD=∠CAD=∠CBD,
∵∠IBD=∠CBI+∠CBD,
∴∠BID=∠IBD
∴ID=BD;
(2)解:连接OA、OD、BD和BI,
∵OA=OD,OI⊥AD
∴AI=ID,
∵I为△ABC内心,
∴∠BAD=∠BCD,
∴弧BD=弧CD,
∵弧CD=弧CD,
∴∠BCD=∠BAD,
∴∠DBI=∠BCD+∠CBI=∠CAD+∠CBI,
=![]() (∠BAC+∠ACB),
(∠BAC+∠ACB),
∵∠DIB=∠DAB+∠ABI=![]() (∠BAC+∠ABC),
(∠BAC+∠ABC),
∴∠DIB=∠DBI,
∴BD=ID=AI,![]() ,
,
故OD⊥BC,记垂足为E,则有BE=![]() BC,
BC,
作IG⊥AB于G,又∠DBE=∠IAG,而BD=AI,
∴Rt△BDE≌Rt△AIG,
于是,AG=BE=![]() BC,但AG=
BC,但AG=![]() (AB+AC﹣BC),
(AB+AC﹣BC),
故AB+AC=2BC,
∴![]() =2.
=2.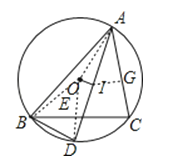
【解析】(1)要证明ID=BD,利用内心的定义可以得到∠ABI=∠CBI,然后利用同弧所对的圆周角相等和三角形的外角等于不相邻的两个外角的和,即可证得∠BID=∠IBD,利用等边对等角即可证得;
(2)作IG⊥AB于G,又∠DBE=∠IAG,而BD=AI,证得:Rt△BDE≌Rt△AIG,则AG=BE=![]() BC,根据直角三角形的内心的性质可得:AG=
BC,根据直角三角形的内心的性质可得:AG=![]() (AB+AC﹣BC),再根据AB+AC=2BC即可求解.
(AB+AC﹣BC),再根据AB+AC=2BC即可求解.
【考点精析】利用三角形的内切圆与内心对题目进行判断即可得到答案,需要熟知三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.