题目内容
【题目】如图,已知抛物线y=﹣![]() x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
x2+bx+4与x轴相交于A、B两点,与y轴相交于点C,若已知A点的坐标为A(﹣2,0).
(1)求抛物线的解析式及它的对称轴;
(2)求点C的坐标,连接AC、BC并求线段BC所在直线的解析式;
(3)在抛物线的对称轴上是否存在点Q,使△ACQ为等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由.

【答案】(1)y=-![]() x2+
x2+![]() x+4,x=3;(2)C(0,4);y=
x+4,x=3;(2)C(0,4);y=![]() x+4.(3)Q1(3,0),Q2(3,4+
x+4.(3)Q1(3,0),Q2(3,4+![]() ),Q3(3,4-
),Q3(3,4-![]() ).
).
【解析】
试题分析:(1)利用待定系数法求出抛物线解析式,利用配方法或利用公式x=![]() 求出对称轴方程;
求出对称轴方程;
(2)在抛物线解析式中,令x=0,可求出点C坐标;令y=0,可求出点B坐标.再利用待定系数法求出直线BD的解析式;
(3)本问为存在型问题.若△ACQ为等腰三角形,则有三种可能的情形,需要分类讨论,逐一计算,避免漏解.
(1)∵抛物线y=-![]() x2+bx+4的图象经过点A(-2,0),
x2+bx+4的图象经过点A(-2,0),
∴-![]() ×(-2)2+b×(-2)+4=0,
×(-2)2+b×(-2)+4=0,
解得:b=![]() ,
,
∴抛物线解析式为 y=-![]() x2+
x2+![]() x+4,
x+4,
又∵y=-![]() x2+
x2+![]() x+4=-
x+4=-![]() (x-3)2+
(x-3)2+![]() ,
,
∴对称轴方程为:x=3.
(2)在y=-![]() x2+
x2+![]() x+4中,令x=0,得y=4,
x+4中,令x=0,得y=4,
∴C(0,4);
令y=0,即-![]() x2+
x2+![]() x+4=0,整理得x2-6x-16=0,解得:x=8或x=-2,
x+4=0,整理得x2-6x-16=0,解得:x=8或x=-2,
∴A(-2,0),B(8,0).
设直线BC的解析式为y=kx+b,
把B(8,0),C(0,4)的坐标分别代入解析式,得:
![]() ,
,
解得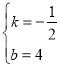 ,
,
∴直线BC的解析式为:y=![]() x+4.
x+4.
∵抛物线的对称轴方程为:x=3,
可设点Q(3,t),则可求得:
AC=![]() ,
,
AQ=![]() ,
,
CQ=![]() .
.
i)当AQ=CQ时,有![]() =
=![]() ,
,
25+t2=t2-8t+16+9,
解得t=0,
∴Q1(3,0);
ii)当AC=AQ时,有![]()
t2=-5,此方程无实数根,
∴此时△ACQ不能构成等腰三角形;
iii)当AC=CQ时,有![]() ,
,
整理得:t2-8t+5=0,
解得:t=4±![]() ,
,
∴点Q坐标为:Q2(3,4+![]() ),Q3(3,4-
),Q3(3,4-![]() ).
).
综上所述,存在点Q,使△ACQ为等腰三角形,点Q的坐标为:Q1(3,0),Q2(3,4+![]() ),Q3(3,4-
),Q3(3,4-![]() ).
).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .
【题目】甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数![]() 与方差s2如下表所示:
与方差s2如下表所示:
甲 | 乙 | 丙 | 丁 | |
平均数 | 561 | 560 | 561 | 560 |
方差s2 | 3.5 | 3.5 | 15.5 | 16.5 |
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择( )
A. 甲 B. 乙 C. 丙 D. 丁

