题目内容
【题目】如图,已知△ABC与△CDE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC.其中正确结论的个数为

A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】
根据题意,结合图形,对选项一一求证,即可得出正确选项.
(1)△ABC和△DCE均是等边三角形,点B,C,E在同一条直线上,∴AC=BC,EC=DC,∠ACB=∠DCE=60°,∴∠ACE=∠BCD=120°.
在△BCD和△ACE中,∵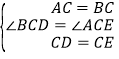 ,∴△BCD≌△ACE,∴AE=BD,故结论①正确;
,∴△BCD≌△ACE,∴AE=BD,故结论①正确;
(2)∵△BCD≌△ECA,∴∠GAC=∠FBC.
又∵∠ACG=∠BCF=60°,AC=BC,∴△ACG≌△BCF,∴AG=BF,故结论②正确;
(3)∵△ACG≌△BCF,∴CG=CF.
∵∠ACB=∠DCE=60°,∴∠ACD=60°,∴△FCG为等边三角形,∴∠FGC=60°,∴∠FGC=∠DCE,∴FG∥BE,故结论③正确;
(4)过C作CN⊥AE于N,CZ⊥BD于Z,则∠CNE=∠CZD=90°.
∵△ACE≌△BCD,∴∠CDZ=∠CEN.
在△CDZ和△CEN中, ,∴△CDZ≌△CEN,∴CZ=CN.
,∴△CDZ≌△CEN,∴CZ=CN.
∵CN⊥AE,CZ⊥BD,∴∠BOC=∠EOC,故结论④正确.
综上所述:四个结论均正确.
故选D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目














