Question

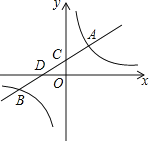
【题目】如图，已知一次函数与反比例函数的图象在第一、第三象限分别交于，两点，直线与轴，轴分别交于两点．

（1）求一次函数和反比例函数的解析式；

（2）比较大小：　 　（填“＞”或“＜”或“＝”）；

（3）直接写出时的取值范围．

Answer 1

【答案】（1）；（2）＝；（3）时的取值范围是或．

【解析】

（1）把A（3，4）代入反比例函数，根据待定系数法即可求得m，得到反比例函数的解析式，然后代入B（a，-2）），求得a，再根据待定系数法求得一次函数的解析式即可；

（2）求得C、D的坐标，利用勾股定理即可判断；

（3）根据图象即可求得．

（1）把代入反比例函数得，

，解得，

∴反比例函数的解析式为；

∵点在反比例函数的图象上，

∴，解得a＝﹣6，

∴，

∵一次函数的图象经过，两点，

∴，解得，

∴一次函数的解析式为；

（2）由一次函数的解析式为可知，，

∴，，

∴，

故答案为:＝；

（3）由图象可知：时的取值范围是或．