题目内容
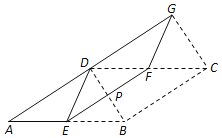
【题目】如图,在平行四边形ABCD中,AD⊥DB,垂足为点D,将平行四边形ABCD折叠,使点B落在点D的位置,点C落在点G的位置,折痕为EF,EF交对角线BD于点P.
(1)连结CG,请判断四边形DBCG的形状,并说明理由;
(2)若AE=BD,求∠EDF的度数.
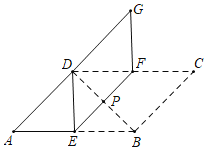
【答案】(1)四边形BCGD是矩形,理由详见解析;(2)∠EDF=120°.
【解析】
(1)根据平行四边形的性质和折叠性质以及矩形的判定解答即可;
(2)根据折叠的性质以及直角三角形的性质和等边三角形的判定与性质解答即可.
解:(1)四边形BCGD是矩形,理由如下,
∵四边形ABCD是平行四边形,
∴BC∥AD,即BC∥DG,
由折叠可知,BC=DG,
∴四边形BCGD是平行四边形,
∵AD⊥BD,
∴∠CBD=90°,
∴四边形BCGD是矩形;
(2)由折叠可知:EF垂直平分BD,
∴BD⊥EF,DP=BP,
∵AD⊥BD,
∴EF∥AD∥BC,
∴![]()
∴AE=BE,
∴DE是Rt△ADB斜边上的中线,
∴DE=AE=BE,
∵AE=BD,
∴DE=BD=BE,
∴△DBE是等边三角形,
∴∠EDB=∠DBE=60°,
∵AB∥DC,
∴∠DBC=∠DBE=60°,
∴∠EDF=120°.

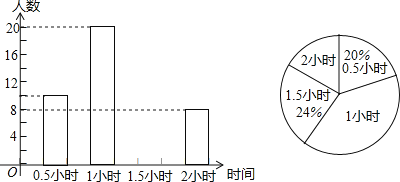
【题目】《国家学生体质健康标准》规定:体质测试成绩达到90.0分及以上的为优秀;达到80.0分至89.9分的为良好;达到60.0分至79.9分的为及格;59.9分及以下为不及格,某校为了了解九年级学生体质健康状况,从该校九年级学生中随机抽取了10%的学生进行体质测试,测试结果如下面的统计表和扇形统计图所示。
各等级学生平均分统计表
等级 | 优秀 | 良好 | 及格 | 不及格 |
平均分 | 92.1 | 85.0 | 69.2 | 41.3 |
各等级学生人数分布扇形统计图

(1)扇形统计图中“不及格”所占的百分比是 ;
(2)计算所抽取的学生的测试成绩的平均分;
(3)若所抽取的学生中所有不及格等级学生的总分恰好等于某一个良好等级学生的分数,请估计该九年级学生中约有多少人达到优秀等级。