Question

【题目】在正方形ABCD中，点E、F在边AB、CD上，点G、H在边AD、CB上，EF和GH相交于点O，∠DGH＝70°，按下列要求分别画出EF

（1）当∠GOE＝90°时，求证：EF＝GH；

（2）当EF＝GH时，画出示意图，直接写出∠GOE的度数．

Answer 1

【答案】（1）见解析；（2）见解析，∠GOE＝90°或50°．

【解析】

（1）作ET⊥CD于T，作HR⊥AD于R，构造两个直角三角形，利用正方形四边相等，四个角都是直角，且∠GOE＝90°，证明这两个直角三角形全等，即可；

（2）同理，构造两个直角三角形，利用正方形四边相等，四个角都是直角，且EF＝GH，证明这两个直角三角形全等，即可求得答案.要注意EF与GH的两种不同的相交情况.

解：（1）如图1，过点E作ET⊥CD于T，过点H作HR⊥AD于R，

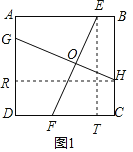
则∠ETF＝∠HRG＝90°

∵四边形ABCD是正方形，

∴AB＝BC，∠A＝∠B＝∠C＝∠D＝90°，AB∥CD，AD∥BC

∴四边形ABHR、四边形BCTE均为矩形

∴HR＝AB＝BC＝ET

∵∠GOE＝90°

∴∠GOF＝90°，∠GOF+∠D＝180°

∵∠DGO+∠DFO+∠GOF+∠D＝360°

∴∠DGO+∠DFO＝180°

∵∠EFT+∠DFO＝180°

∴∠DGO＝∠EFT

∴△EFT≌△HGR（AAS）

∴EF＝GH；

（2）如图2，过点E作ET⊥CD于T，过点H作HR⊥AD于R，

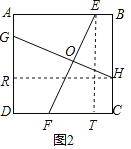
则∠ETF＝∠HRG＝90°

∵四边形ABCD是正方形，

∴AB＝BC，∠A＝∠B＝∠C＝∠D＝90°，AB∥CD，AD∥BC

∴四边形ABHR、四边形BCTE均为矩形

∴HR＝AB＝BC＝ET

∵EF＝GH

∴Rt△EFT≌Rt△HGR（HL）

∴∠EFT＝∠HGR

∵∠EFT+∠DFO＝180°

∴∠HGR+∠DFO＝180°

∵∠HGR+∠DFO+∠GOF+∠D＝360°

∴∠GOF+∠D＝180°

∴∠GOF＝90°

∴∠GOE＝90°

如图3，过点E作ET⊥CD于T，过点H作HR⊥AD于R，

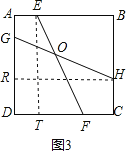
则∠ETF＝∠HRG＝90°

∵四边形ABCD是正方形，

∴AB＝BC，∠A＝∠B＝∠C＝∠D＝90°，AB∥CD，AD∥BC

∴四边形ABHR、四边形BCTE均为矩形

∴HR＝AB＝BC＝ET

∵EF＝GH

∴Rt△EFT≌Rt△HGR（HL）

∴∠EFT＝∠HGR＝70°

∵∠HGR+∠DFO+∠GOF+∠D＝360°

∴∠FOG＝130°

∴∠GOE＝180°﹣∠FOG＝180°﹣130°＝50°

综上所述，∠GOE＝90°或50°．