��Ŀ����
����Ŀ���밴Ҫ�������������С�⣨������ͼ��Ҫ��߹���ͼ��.
��1����ͼ1��AB=AC.�������߶�һ�����ڡ�BAC��______����ֱ�߶Գƣ��뻭����ֱ��.
��2����ͼ2����֪�߶�AB�͵�C.�����߶�CD��ʹ����AB����Գƣ���A��C�ǶԳƵ㣬�Գ������߶�AC��______.
��3����ͼ3������λ�ã�������Գƣ��������߶�AB��CD��AB=CD.���ܴӣ�1������2�����л�õ���ʾ��������һ���߶���������Գ�ʹ�����غ�������ܣ��뻭��ͼ�β���Ҫ�����������裻������ܣ���˵������.

���𰸡���1����ƽ���ߣ���ͼ����������2����ֱƽ���ߣ���ͼ����������3���ܣ���ͼ������.
��������
��1��������Գ���������BAC�Ľ�ƽ�����ɣ���2������AC����AC�Ĵ�ֱƽ���ߣ���Ϊ�Գ��ᣬ��B����ڶԳ���ĶԳƵ�D������CD��Ϊ����3������BD����BD�Ĵ�ֱƽ���ߣ���Ϊ�Գ��ᣬ����C���ڶԳ���ĶԳƵ�E������BE������ABE�Ľ�ƽ����Ϊ�Գ��ᣬ���ɶ�����һ���߶���������Գ�ʹ�����غ�.
��1����ͼ������BAC�Ľ�ƽ���ߣ����ǡ�BAC�ĶԳ��ᣬ
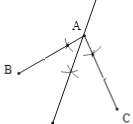
�ʴ�Ϊ����ƽ����
��2����ͼ������AC����AC�Ĵ�ֱƽ���ߣ���Ϊ�Գ��ᣬ��B����ڶԳ���ĶԳƵ�D������CD��Ϊ����.
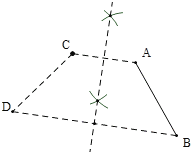
�ʴ�Ϊ����ֱƽ����
��3������BD����BD�Ĵ�ֱƽ���ߣ���Ϊ�Գ��ᣬ����C���ڶԳ���ĶԳƵ�E������BE������ABE�Ľ�ƽ����Ϊ�Գ��ᣬ
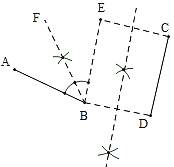
���ܶ�����һ���߶���������Գ�ʹ�����غ�.

 Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�
Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�����Ŀ��ijУ��1500��ѧ����Ϊ�˽�ȫУѧ������ѧ��ʽ����У��ѧ��ȤС����ȫУ�����ȡ��100��ѧ�����г������飮�����������ݣ��õ�����ͼ����Ƶ���ֲ����в��ֻ��DZ�īˮ��ס����
ijУ100��ѧ����ѧ��ʽƵ���ֲ���
��ʽ | ���� | Ƶ�� |
���� | ������ | 15 |
�ﳵ | ���������� | 29 |
�˹�����ͨ���� | ������������ | 30 |
��˽�ҳ� | ||
���� | ||
�ϼ� | 100 |
��1�����ε���ĸ������� ����
��2����Ƶ���ֲ����У�����˽�ҳ������ֶ�Ӧ��Ƶ����
��3������Ƹ�У1500��ѧ���У�ѡ���ﳵ���˹����Ͳ�����ѧ��һ���ж����ˣ�






