ЬтФПФкШн
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=ax2+cЙ§ЕуЃЈЉ2ЃЌ2ЃЉЃЌЃЈ4ЃЌ5ЃЉЃЌЙ§ЖЈЕуFЃЈ0ЃЌ2ЃЉЕФжБЯпlЃКy=kx+2гыХзЮяЯпНЛгкAЁЂBСНЕуЃЌЕуBдкЕуAЕФгвВрЃЌЙ§ЕуBзїxжсЕФДЙЯпЃЌДЙзуЮЊCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБЕуBдкХзЮяЯпЩЯдЫЖЏЪБЃЌХаЖЯЯпЖЮBFгыBCЕФЪ§СПЙиЯЕЃЈЃОЁЂЃМЁЂ=ЃЉЃЌВЂжЄУїФуЕФХаЖЯЃЛ
ЃЈ3ЃЉPЮЊyжсЩЯвЛЕуЃЌвдBЁЂCЁЂFЁЂPЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЃЌЩшЕуPЃЈ0ЃЌmЃЉЃЌЧѓздШЛЪ§mЕФжЕЃЛ
ЃЈ4ЃЉШєk=1ЃЌдкжБЯпlЯТЗНЕФХзЮяЯпЩЯЪЧЗёДцдкЕуQЃЌЪЙЕУЁїQBFЕФУцЛ§зюДѓЃПШєДцдкЃЌЧѓГіЕуQЕФзјБъМАЁїQBFЕФзюДѓУцЛ§ЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉ
НтЃКАбЕуЃЈЉ2ЃЌ2ЃЉЃЌЃЈ4ЃЌ5ЃЉДњШыy=ax2+cЕУ ![]() ЃЌНтЕУ
ЃЌНтЕУ ![]() ЃЌ
ЃЌ
ЫљвдХзЮяЯпНтЮіЪНЮЊy= ![]() x2+1ЃЛ
x2+1ЃЛ
ЃЈ2ЃЉ
НтЃКBF=BCЃЎ
РэгЩШчЯТЃК
ЩшBЃЈxЃЌ ![]() x2+1ЃЉЃЌЖјFЃЈ0ЃЌ2ЃЉЃЌ
x2+1ЃЉЃЌЖјFЃЈ0ЃЌ2ЃЉЃЌ
ЁрBF2=x2+ЃЈ ![]() x2+1Љ2ЃЉ2=x2+ЃЈ
x2+1Љ2ЃЉ2=x2+ЃЈ ![]() x2Љ1ЃЉ2=ЃЈ
x2Љ1ЃЉ2=ЃЈ ![]() x2+1ЃЉ2ЃЌ
x2+1ЃЉ2ЃЌ
ЁрBF= ![]() x2+1ЃЌ
x2+1ЃЌ
ЁпBCЁЭxжсЃЌ
ЁрBC= ![]() x2+1ЃЌ
x2+1ЃЌ
ЁрBF=BCЃЛ
ЃЈ3ЃЉ
НтЃКШчЭМ1ЃЌ
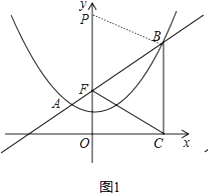
mЮЊздШЛЪ§ЃЌдђЕуPдкFЕуЩЯЗНЃЌ
ЁпвдBЁЂCЁЂFЁЂPЮЊЖЅЕуЕФЫФБпаЮЪЧСтаЮЃЌ
ЁрCB=CF=PFЃЌ
ЖјCB=FBЃЌ
ЁрBC=CF=BFЃЌ
ЁрЁїBCFЮЊЕШБпШ§НЧаЮЃЌ
ЁрЁЯBCF=60ЁуЃЌ
ЁрЁЯOCF=30ЁуЃЌ
дкRtЁїOCFжаЃЌCF=2OF=4ЃЌ
ЁрPF=CF=4ЃЌ
ЁрPЃЈ0ЃЌ6ЃЉЃЌ
МДздШЛЪ§mЕФжЕЮЊ6ЃЛ
ЃЈ4ЃЉ
НтЃКзїQEЁЮyжсНЛABгкEЃЌШчЭМ2ЃЌ
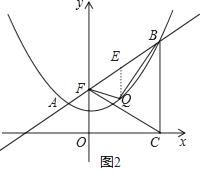
ЕБk=1ЪБЃЌвЛДЮКЏЪ§НтЮіЪНЮЊy=x+2ЃЌ
НтЗНГЬзщ 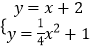 ЕУ
ЕУ ![]() Лђ
Лђ ![]() ЃЌдђBЃЈ1+
ЃЌдђBЃЈ1+ ![]() ЃЌ3+
ЃЌ3+ ![]() ЃЉЃЌ
ЃЉЃЌ
ЩшQЃЈtЃЌ ![]() t2+1ЃЉЃЌдђEЃЈtЃЌt+2ЃЉЃЌ
t2+1ЃЉЃЌдђEЃЈtЃЌt+2ЃЉЃЌ
ЁрEQ=t+2ЉЃЈ ![]() t2+1ЃЉ=Љ
t2+1ЃЉ=Љ ![]() t2+t+1ЃЌ
t2+t+1ЃЌ
ЁрSЁїQBF=SЁїEQF+SЁїEQB= ![]() ЃЈ1+
ЃЈ1+ ![]() ЃЉEQ=
ЃЉEQ= ![]() ЃЈ1+
ЃЈ1+ ![]() ЃЉЃЉЃЈЉ
ЃЉЃЉЃЈЉ ![]() t2+t+1ЃЉ=Љ
t2+t+1ЃЉ=Љ ![]() ЃЈtЉ2ЃЉ2+
ЃЈtЉ2ЃЉ2+ ![]() +1ЃЌ
+1ЃЌ
ЕБt=2ЪБЃЌSЁїQBFгазюДѓжЕЃЌзюДѓжЕЮЊ ![]() +1ЃЌДЫЪБQЕузјБъЮЊЃЈ2ЃЌ2ЃЉЃЎ
+1ЃЌДЫЪБQЕузјБъЮЊЃЈ2ЃЌ2ЃЉЃЎ
ЁОНтЮіЁПЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈЧѓХзЮяЯпНтЮіЪНЃЛЃЈ2ЃЉЩшBЃЈxЃЌ ![]() x2+1ЃЉЃЌЖјFЃЈ0ЃЌ2ЃЉЃЌРћгУСНЕуМфЕФОрРыЙЋЪНЕУЕНBF2=x2+ЃЈ
x2+1ЃЉЃЌЖјFЃЈ0ЃЌ2ЃЉЃЌРћгУСНЕуМфЕФОрРыЙЋЪНЕУЕНBF2=x2+ЃЈ ![]() x2+1Љ2ЃЉ2=ЃЌдйРћгУХфЗНЗЈПЩЕУЕНBF=
x2+1Љ2ЃЉ2=ЃЌдйРћгУХфЗНЗЈПЩЕУЕНBF= ![]() x2+1ЃЌгЩгкBC=
x2+1ЃЌгЩгкBC= ![]() x2+1ЃЌЫљвдBF=BCЃЛЃЈ3ЃЉШчЭМ1ЃЌРћгУСтаЮЕФаджЪЕУЕНCB=CF=PFЃЌМгЩЯCB=FBЃЌдђПЩХаЖЯЁїBCFЮЊЕШБпШ§НЧаЮЃЌЫљвдЁЯBCF=60ЁуЃЌдђЁЯOCF=30ЁуЃЌгкЪЧПЩМЦЫуГіCF=4ЃЌЫљвдPF=CF=4ЃЌДгЖјЕУЕНздШЛЪ§mЕФжЕЮЊ6ЃЛЃЈ4ЃЉзїQEЁЮyжсНЛABгкEЃЌШчЭМ2ЃЌЯШНтЗНГЬзщ
x2+1ЃЌЫљвдBF=BCЃЛЃЈ3ЃЉШчЭМ1ЃЌРћгУСтаЮЕФаджЪЕУЕНCB=CF=PFЃЌМгЩЯCB=FBЃЌдђПЩХаЖЯЁїBCFЮЊЕШБпШ§НЧаЮЃЌЫљвдЁЯBCF=60ЁуЃЌдђЁЯOCF=30ЁуЃЌгкЪЧПЩМЦЫуГіCF=4ЃЌЫљвдPF=CF=4ЃЌДгЖјЕУЕНздШЛЪ§mЕФжЕЮЊ6ЃЛЃЈ4ЃЉзїQEЁЮyжсНЛABгкEЃЌШчЭМ2ЃЌЯШНтЗНГЬзщ 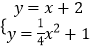 ЕУBЃЈ1+
ЕУBЃЈ1+ ![]() ЃЌ3+
ЃЌ3+ ![]() ЃЉЃЌЩшQЃЈtЃЌ
ЃЉЃЌЩшQЃЈtЃЌ ![]() t2+1ЃЉЃЌдђEЃЈtЃЌt+2ЃЉЃЌдђEQ=Љ
t2+1ЃЉЃЌдђEЃЈtЃЌt+2ЃЉЃЌдђEQ=Љ ![]() t2+t+1ЃЌдђSЁїQBF=SЁїEQF+SЁїEQB=
t2+t+1ЃЌдђSЁїQBF=SЁїEQF+SЁїEQB= ![]() ЃЈ1+
ЃЈ1+ ![]() ЃЉEQ=
ЃЉEQ= ![]() ЃЈ1+
ЃЈ1+ ![]() ЃЉЃЉЃЈЉ
ЃЉЃЉЃЈЉ ![]() t2+t+1ЃЉЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтЃЎ
t2+t+1ЃЉЃЌШЛКѓИљОнЖўДЮКЏЪ§ЕФаджЪНтОіЮЪЬтЃЎ

ЁОЬтФПЁПФГаЃОіЖЈМгЧПг№УЋЧђЁЂРКЧђЁЂЦЙХвЧђЁЂХХЧђЁЂзуЧђЮхЯюЧђРрдЫЖЏЃЌУПЮЛЭЌбЇБиаыЧвжЛФмбЁдёвЛЯюЧђРрдЫЖЏЃЌЖдИУаЃбЇЩњЫцЛњГщШЁ10%НјааЕїВщЃЌИљОнЕїВщНсЙћЛцжЦСЫШчЯТВЛЭъећЕФЦЕЪ§ЗжВМБэКЭЩШаЮЭГМЦЭМЃК
дЫЖЏЯюФП | ЦЕЪ§ЃЈШЫЪ§ЃЉ |
г№УЋЧђ | 30 |
РКЧђ | a |
ЦЙХвЧђ | 36 |
ХХЧђ | b |
зуЧђ | 12 |

ЧыИљОнвдЩЯЭМБэаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЦЕЪ§ЗжВМБэжаЕФa= ЃЌ b=ЃЛ
ЃЈ2ЃЉдкЩШаЮЭГМЦЭМжаЃЌЁАХХЧђЁБЫљдкЕФЩШаЮЕФдВаФНЧЮЊЖШЃЛ
ЃЈ3ЃЉШЋаЃгаЖрЩйУћбЇЩњбЁдёВЮМгЦЙХвЧђдЫЖЏЃП