题目内容
【题目】在Rt△ABC中,∠ACB=90°,点D与点B在AC同侧,∠DAC>∠BAC,且DA=DC,过点B作BE∥DA交DC于点E,M为AB的中点,连接MD,ME.
(1)如图1,当∠ADC=90°时,线段MD与ME的数量关系是;
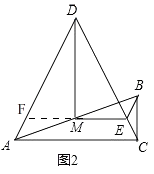
(2)如图2,当∠ADC=60°时,试探究线段MD与ME的数量关系,并证明你的结论;
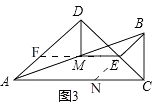
(3)如图3,当∠ADC=α时,求 ![]() 的值.
的值.
【答案】
(1)MD=ME
(2)
解:MD= ![]() ME,理由:
ME,理由:
如图2,延长EM交AD于F,
∵BE∥DA,
∴∠FAM=∠EBM,
∵AM=BM,∠AMF=∠BME,
∴△AMF≌△BME,
∴AF=BE,MF=ME,
∵DA=DC,∠ADC=60°,
∴∠BED=∠ADC=60°,∠ACD=60°,
∵∠ACB=90°,
∴∠ECB=30°,
∴∠EBC=∠BED﹣∠ECB=30°=∠ECB,
∴CE=BE,
∴AF=CE,
∵DA=DC,
∴DF=DE,
∴DM⊥EF,DM平分∠ADC,
∴∠MDE=30°,
在Rt△MDE中,tan∠MDE= ![]() ,
,
∴MD= ![]() ME.
ME.
(3)
解:如图3,延长EM交AD于F,
∵BE∥DA,
∴∠FAM=∠EBM,
∵AM=BM,∠AMF=∠BME,
∴△AMF≌△BME,
∴AF=BE,MF=ME,
延长BE交AC于点N,
∴∠BNC=∠DAC,
∵DA=DC,
∴∠DCA=∠DAC,
∴∠BNC=∠DCA,
∵∠ACB=90°,
∴∠ECB=∠EBC,
∴CE=BE,
∴AF=CE,
∴DF=DE,
∴DM⊥EF,DM平分∠ADC,
∵∠ADC=α,
∴∠MDE= ![]() ,
,
在Rt△MDE中, ![]() =tan∠MDE=tan
=tan∠MDE=tan ![]() .
.
【解析】解:(1.)如图1,延长EM交AD于F,
∵BE∥DA,
∴∠FAM=∠EBM,
∵AM=BM,∠AMF=∠BME,
∴△AMF≌△BME,
∴AF=BE,MF=ME,
∵DA=DC,∠ADC=90°,
∴∠BED=∠ADC=90°,∠ACD=45°,
∵∠ACB=90°,
∴∠ECB=45°,
∴∠EBC=∠BED﹣∠ECB=45°=∠ECB,
∴CE=BE,
∴AF=CE,
∵DA=DC,
∴DF=DE,
∴DM⊥EF,DM平分∠ADC,
∴∠MDE=45°,
∴MD=ME,
所以答案是MD=ME;

 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案





