题目内容
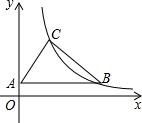 如图,Rt△ABC 中,∠C=90°,AC=6,BC=8,点A在y轴上,B,C在反比例函数
如图,Rt△ABC 中,∠C=90°,AC=6,BC=8,点A在y轴上,B,C在反比例函数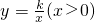 的图象上,且AB∥x轴,则k的值为
的图象上,且AB∥x轴,则k的值为
- A.25
- B.26
- C.27
- D.28
C
分析:首先过点C作CF⊥AB交AB于点N,交x轴于点F,作BE⊥x轴于点E,利用勾股定理表示出B,C点坐标,进而得出关于y的等式求出即可.
解答: 解:过点C作CF⊥AB交AB于点N,交x轴于点F,作BE⊥x轴于点E,
解:过点C作CF⊥AB交AB于点N,交x轴于点F,作BE⊥x轴于点E,
∵Rt△ABC 中,∠C=90°,AC=6,BC=8,
∴AB=10,CN=4.8,
∴AN=3.6,
∴设C点坐标为:(3.6,y+4.8),B点坐标为;(10,y),
∴3.6×(y+4.8)=10y
解得:y=2.7,
∴k的值为;10×2.7=27.
故选:C.
点评:此题主要考查了反比例函数综合以及勾股定理等知识,根据已知得出B,C点坐标是解题关键.
分析:首先过点C作CF⊥AB交AB于点N,交x轴于点F,作BE⊥x轴于点E,利用勾股定理表示出B,C点坐标,进而得出关于y的等式求出即可.
解答:
 解:过点C作CF⊥AB交AB于点N,交x轴于点F,作BE⊥x轴于点E,
解:过点C作CF⊥AB交AB于点N,交x轴于点F,作BE⊥x轴于点E,∵Rt△ABC 中,∠C=90°,AC=6,BC=8,
∴AB=10,CN=4.8,
∴AN=3.6,
∴设C点坐标为:(3.6,y+4.8),B点坐标为;(10,y),
∴3.6×(y+4.8)=10y
解得:y=2.7,
∴k的值为;10×2.7=27.
故选:C.
点评:此题主要考查了反比例函数综合以及勾股定理等知识,根据已知得出B,C点坐标是解题关键.

练习册系列答案
相关题目
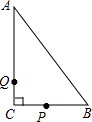 如图,Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从B点出发,以2cm/s的速度向点C运动,点Q从C点出发,以1cm/s的速度向点A运动.若P,Q同时出发,则经过
如图,Rt△ABC中,∠C=90°,BC=6cm,AC=8cm,点P从B点出发,以2cm/s的速度向点C运动,点Q从C点出发,以1cm/s的速度向点A运动.若P,Q同时出发,则经过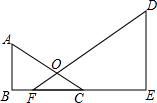 已知,如图,Rt△ABC中∠B=90°,Rt△DEF中∠E=90°,OF=OC,AB=6,BF=2,CE=8,CA=0,DE=15.
已知,如图,Rt△ABC中∠B=90°,Rt△DEF中∠E=90°,OF=OC,AB=6,BF=2,CE=8,CA=0,DE=15.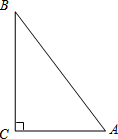 (2013•封开县一模)如图,Rt△ABC的直角边BC=8,AC=6
(2013•封开县一模)如图,Rt△ABC的直角边BC=8,AC=6