题目内容
如图,Rt△ABC的直角边AC落在数轴上,点A表示的数是2,以A为旋转中心逆时针旋转△ABC.(1)当∠B=70°时,则旋转角度至少是
(2)若AB=
| 5 |
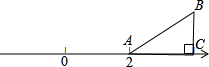
分析:(1)由以A为旋转中心逆时针旋转△ABC,点B的对应点落在数轴上,则旋转角等于∠OAB,而B=70°,则∠BAC=90°-70°=20°,得到∠OAB=180°-20°=160°,即即旋转角度至少是160°,点B的对应点落在数轴上;
(2)点B的对应点B1第一次落在数轴上时,AB1=AB=
,得到OB1=AB1-OA=
-2,则B1表示的数为2-
.
(2)点B的对应点B1第一次落在数轴上时,AB1=AB=
| 5 |
| 5 |
| 5 |
解答:解:(1)∵以A为旋转中心逆时针旋转△ABC,点B的对应点落在数轴上,则旋转角等于∠OAB,
而∠B=70°,则∠BAC=90°-70°=20°,
∴∠OAB=180°-20°=160°,
即旋转角度至少是160°,点B的对应点落在数轴上;
(2)点B的对应点B1第一次落在数轴上时,AB1=AB=
,
∴OB1=AB1-OA=
-2,
而点B1在数轴的负半轴,
所以B1表示的数为2-
.
故答案为:160°;2-
.
而∠B=70°,则∠BAC=90°-70°=20°,
∴∠OAB=180°-20°=160°,
即旋转角度至少是160°,点B的对应点落在数轴上;
(2)点B的对应点B1第一次落在数轴上时,AB1=AB=
| 5 |
∴OB1=AB1-OA=
| 5 |
而点B1在数轴的负半轴,
所以B1表示的数为2-
| 5 |
故答案为:160°;2-
| 5 |
点评:本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了数轴上点与实数的关系.

练习册系列答案
相关题目
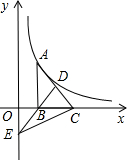 如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延长线交y轴负半轴于E,双曲线
如图,Rt△ABC的直角边BC在x轴正半轴上,斜边AC边上的中线BD反向延长线交y轴负半轴于E,双曲线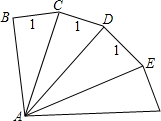 如图,Rt△ABC的两直角边分别为1,2,以Rt△ABC的斜边AC为一直角边,另一直角边为1画第二个△ACD;在以△ACD的斜边AD为一直角边,另一直角边长为1画第三个△ADE;…,依此类推,第n个直角三角形的斜边长是
如图,Rt△ABC的两直角边分别为1,2,以Rt△ABC的斜边AC为一直角边,另一直角边为1画第二个△ACD;在以△ACD的斜边AD为一直角边,另一直角边长为1画第三个△ADE;…,依此类推,第n个直角三角形的斜边长是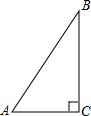 如图,Rt△ABC的斜边AB=10cm,
如图,Rt△ABC的斜边AB=10cm,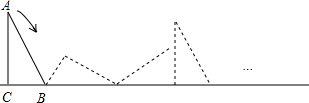
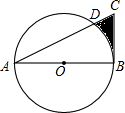 如图,Rt△ABC的一条直角边AB是⊙O的直径,AB=8,斜边交⊙O于D,∠A=30°,求阴影部分的面积.
如图,Rt△ABC的一条直角边AB是⊙O的直径,AB=8,斜边交⊙O于D,∠A=30°,求阴影部分的面积.