Question

【题目】如图，点O在∠APB的平分线上，⊙O与PA相切于点C．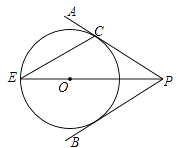

（1）求证：直线PB与⊙O相切；
（2）PO的延长线与⊙O交于点E．若⊙O的半径为3，PC=4．求弦CE的长．

Answer 1

【答案】
（1）证明：连接OC，作OD⊥PB于D点．

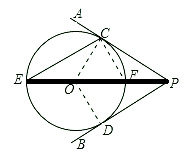
∵⊙O与PA相切于点C， ∴OC⊥PA

（2）解：设PO交⊙O于F，连接CF．

∵OC=3，PC=4，∴PO=5，PE=8．

∵⊙O与PA相切于点C， ∴∠PCF=∠E．

又∵∠CPF=∠EPC， ∴△PCF∽△PEC，

∴CF：CE=PC：PE=4：8=1：2．

∵EF是直径， ∴∠ECF=90°．

设CF=x，则EC=2x．

则x2+（2x）2=62， 解得x= ．

则EC=2x= ．

【解析】要证明直线PB与⊙O相切，添加辅助线连接OC，作OD⊥PB于D点，再证明OD是圆的半径，根据角平分线上的点到角两边的距离相等及切线的性质，易证得结论。
（2）根据已知易证得△PCF∽△PEC，得出对应边成比例，证出CF：CE=1：2．再根据EF是直径得出△CEF是直角三角形，利用勾股定理求解即可。