题目内容
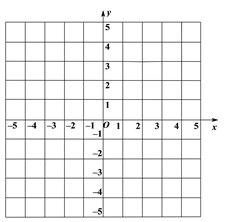
【题目】如图,在平面直角坐标中,点![]() 为坐标原点,
为坐标原点,![]() 的三个顶点坐标分别为
的三个顶点坐标分别为![]() ,
,![]() ,
,![]() ,
,![]() 且
且![]() ,其中
,其中![]() ,
,![]() 满足
满足![]() .
.



(1)求点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 从点
从点![]() 出发,以每秒1个单位长度的速度沿
出发,以每秒1个单位长度的速度沿![]() 轴负方向运动,设点
轴负方向运动,设点![]() 的运动时间为
的运动时间为![]() 秒.连接
秒.连接![]() 、
、![]() ,用含有
,用含有![]() 的式子表示
的式子表示![]() 的面积为
的面积为![]() (直接写出
(直接写出![]() 的取值范围);
的取值范围);
(3)在(2)的条件下,是否存在![]() 的值,使得
的值,使得![]() ,若存在,请求出
,若存在,请求出![]() 的值,并直接写出
的值,并直接写出![]() 中点
中点![]() 的坐标;若不存,请说明理由.
的坐标;若不存,请说明理由.
【答案】(1)A(0,4),C(3,0);(2)S=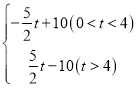 ;(3)存在,满足条件的t的值为
;(3)存在,满足条件的t的值为![]() 或36,点Q的坐标为
或36,点Q的坐标为![]() 或
或![]() .
.
【解析】
(1)解方程组求出m,n即可解决问题.
(2)分两种情形:如图1中,当0<t<4时,如图2中,当t>4时,根据S=![]() BCOP求解即可.
BCOP求解即可.
(3)分两种情形分别构建方程求解即可.
解:(1)由![]() ,
,
解得:![]() ,
,
∴A(0,4),C(3,0);
(2)如图1中,当0<t<4时,
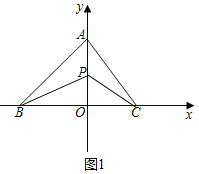
S=![]() BCOP=
BCOP=![]() ×5×(4-t)=-
×5×(4-t)=-![]() t+10.
t+10.
如图2中,当t>4时,
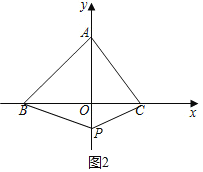
S=![]() BCOP=
BCOP=![]() ×5×(t-4)=
×5×(t-4)=![]() t-10.
t-10.
综上所述,S=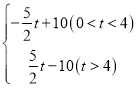 ,
,
(3)当![]() 时,由题意,
时,由题意,![]() ,
,
解得![]() ,
,
此时,![]() ,
,
![]() ,
,
![]() ,
,
![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,
当![]() 时,由题意,
时,由题意,![]() ,
,
解得![]() ,
,
此时![]() ,
,
![]() ,
,
![]() ,
,
![]() 的中点
的中点![]() 的坐标为
的坐标为![]() .
.
综上所述,满足条件的![]() 的值为
的值为![]() 或36.点
或36.点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
相关题目