题目内容
如图,一次函数y=kx+b的图象与反比例函数 的图象交于A(-2,1),B(1,n)两点.
的图象交于A(-2,1),B(1,n)两点.
(1)求反比例函数和一次函数的解析式;(6分)
(2)根据图象写出使一次函数的值大于反比例函数的值的x的取值范围.(4分)
(1)y=-x-1;(2)x<-2或0<x<1.
解析试题分析:(1)根据题意先求得m,再求出n,然后代入y=kx+b求得k、b即可;(2)要使一次函数的值大于反比例函数的值,即使一次函数的图象在反比例函数的图象的上方时,再得出此时x的取值范围.
试题解析:(1)∵反比例函数 的图象经过点A(-2,1),∴
的图象经过点A(-2,1),∴ ,即m=-2.
,即m=-2.
∴反比例函数的解析式为 .
.
又∵反比例函数 的图象经过点B(1,n),∴
的图象经过点B(1,n),∴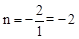 . ∴B(1,-2).
. ∴B(1,-2).
∵一次函数y=kx+b的图象经过A、B两点,∴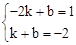 ,解得
,解得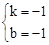 .
.
∴一次函数的解析式为y=-x-1.
(2)当x<-2或0<x<1时,一次函数的值大于反比例函数的值.
考点:1.反比例函数与一次函数的交点问题;2.曲线上点的坐标与方程的关系.

练习册系列答案
相关题目
 的图象与反比例函数
的图象与反比例函数 的图象交于A(1,4)、B(﹣2,m)两点,
的图象交于A(1,4)、B(﹣2,m)两点,  的解集.
的解集.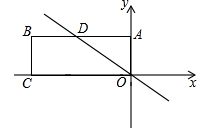
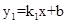 的图象与函数
的图象与函数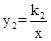 (
(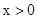 )的图象交于点A(2,1)、B,与y轴交于点C(0,3).
)的图象交于点A(2,1)、B,与y轴交于点C(0,3).
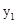 的表达式和点B的坐标;
的表达式和点B的坐标;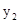 的大小.
的大小.
 吨,应交水费
吨,应交水费 元.
元.
 时,求∠ODB的正切值.
时,求∠ODB的正切值.