题目内容
【题目】阅读下列材料：
解答“已知x﹣y=2，且x＞1，y＜0，试确定x+y的取值范围”有如下解法：
解：∵x﹣y=2，又∵x＞1，∴y+2＞1，即y＞﹣1
又y＜0，∴﹣1＜y＜0．…①
同理得：1＜x＜2．…②
由①+②得﹣1+1＜y+x＜0+2，∴x+y的取值范围是0＜x+y＜2．
请按照上述方法，完成下列问题：
已知关于x、y的方程组
的解都为非负数．
（1）求a的取值范围；
（2）已知2a﹣b=1，且，求a+b的取值范围；
（3）已知a﹣b=m（m是大于1的常数），且b≤1，求2a+b最大值．（用含m的代数式表示）
【答案】（1）
；（2）
；（3）最大值为3+2m．
【解析】试题分析：(1)、首先求出方程组的解，然后根据解为非负数得出a的取值范围；(2)、根据题意得出a=
，然后根据a的取值范围得出b的取值范围，从而得出答案；(3)、根据a=m+b以及a的取值范围得出b的取值范围，然后得出最值.
试题解析：(1)、因为关于x、y的方程组
的解都为非负数，
解得：
，可得：
， 解得：
；
(2)、由2a﹣b=1，可得：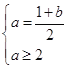
， 可得：
，解得：
， 所以；
(3)、
，所以
，可得：
，
可得：
，同理可得：
，
所以可得：
最大值为3+2m．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
