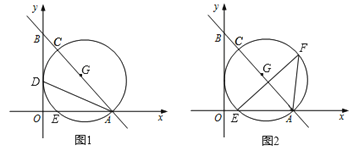题目内容
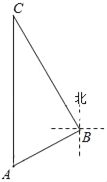
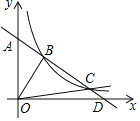
【题目】如图,在平面直角坐标系中,直线BC与y轴交于点A(0,4),与x轴交于点D,点B,C是反比列函数y=![]() (x>0)图象上的点,OB⊥BC于点B,∠BOD=60°.
(x>0)图象上的点,OB⊥BC于点B,∠BOD=60°.
(1)求直线AB的解析式;
(2)求反比例函数的解析式;
(3)若△AOB的面积为S1,△BOC的面积为S2,△DOC的面积为S3,直接写出S1,S2,S3的一个数量关系式:
【答案】(1)y=﹣![]() x+4;(2)y=
x+4;(2)y=![]() ;(3)S1+S3=S2.
;(3)S1+S3=S2.
【解析】
(1)解直角三角形求得OD,得出D的坐标,然后根据待定系数法即可求得;
(2)解直角三角形求得AB,利用勾股定理求得AD,进而求得S△AOB=2![]() ,S△BOD=6
,S△BOD=6![]() ,然后根据三角形面积公式求得B的坐标,代入y=
,然后根据三角形面积公式求得B的坐标,代入y=![]() (x>0)求得k即可;
(x>0)求得k即可;
(3)解析式联立求得C的坐标,进而求得S3=2,即可求得S2=4,从而求得S1+S3=S2.
解:∵A(0,4),
∴OA=4,
∵∠BOD=60°.
∴∠AOB=30°,
∵OB⊥BC于点B,
∴∠ABO=90°,
∴∠OAD=60°,
∴OD=![]() OA=4
OA=4![]() ,
,
∴D(4![]() ,0),
,0),
设直线AB的解析式为y=kx+b,
∴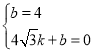 ,解得
,解得 ,
,
∴直线AB的解析式为y=﹣![]() x+4;
x+4;
(2)∵∠AOB=30°,OA=4,
∴AB=![]() OA=2,OB=
OA=2,OB=![]() OA=2
OA=2![]() ,
,
∵![]() OAOD=
OAOD=![]() ADOB,
ADOB,
∴AD=![]() =
=![]() =8,
=8,
∴BD=AD﹣AB=6,
∵S△AOD=![]() =8
=8![]() ,
,
∴S△AOB=![]() ×8
×8![]() =2
=2![]() ,S△BOD=
,S△BOD=![]() ×8
×8![]() =6
=6![]() ,
,
设B(m,n),
∴S△AOB=![]() =2
=2![]() ,S△BOD=
,S△BOD=![]() =6
=6![]() ,
,
∴![]() =2
=2![]() ,
,![]() =6
=6![]() ,
,
解得m=![]() ,n=3,
,n=3,
∴B(![]() ,3),
,3),
∵点B是反比列函数y=![]() (x>0)图象上的点,
(x>0)图象上的点,
∴k=![]() =3
=3![]() ,
,
∴反比例函数的解析式为y=![]() ;
;
(3)解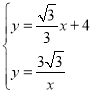 得
得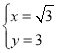 和
和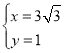 ,
,
∴C(3![]() ,1),
,1),
∴S△COD=![]() =
=![]() =2
=2![]() ,
,
∴S△BOC=6﹣2=4,
∵S1=2,S2=4,S3=2,
∴S1+S3=S2.
故答案为S1+S3=S2.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案【题目】某市在开展线上教学活动期间,为更好地组织初中学生居家体育锻炼,随机抽取了部分初中学生对“最喜爱的体育锻炼项目”进行线上问卷调查(每人必须且只选其中一项),得到如下两幅不完整的统计图表,请根据图表信息回答下列问题:
![]()
类别 | 项 目 | 人数 |
A | 跳绳 | 59 |
B | 健身操 | ▲ |
C | 俯卧撑 | 31 |
D | 开合跳 | ▲ |
E | 其它 | 22 |

(1)求参与问卷调查的学生总人数.
(2)在参与问卷调查的学生中,最喜爱“开合跳”的学生有多少人?
(3)该市共有初中学生约8000人,估算该市初中学生中最喜爱“健身操”的人数.