题目内容
已知二次函数y=x2-4x+3和一次函数y=x+1，则它们交点的个数是
- A.1个
- B.2个
- C.3个
- D.没有交点
B
分析：将两函数解析式联立，列方程组，求方程组解的个数．
解答：由题意得：x2-4x+3=x+1，
整理得：x2-5x+2=0
∵△=25-8＞0
∴x2-5x+2=0有两个不相等的实数根，
∴二次函数y=x2-4x+3和一次函数y=x+1有两个交点，
故选B．
点评：本题考查了二次函数的性质．求函数图象的交点坐标，就是将两函数解析式联立，求方程组的解．
分析：将两函数解析式联立，列方程组，求方程组解的个数．
解答：由题意得：x2-4x+3=x+1，
整理得：x2-5x+2=0
∵△=25-8＞0
∴x2-5x+2=0有两个不相等的实数根，
∴二次函数y=x2-4x+3和一次函数y=x+1有两个交点，
故选B．
点评：本题考查了二次函数的性质．求函数图象的交点坐标，就是将两函数解析式联立，求方程组的解．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
已知二次函数y=x2+（2a+1）x+a2-1的最小值为0，则a的值是（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
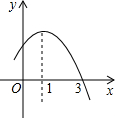已知二次函数y=-x2+2x+m的部分图象如图所示，则关于x的一元二次方程-x2+2x+m=0的解为（ ）| A、x1=1，x2=3 | B、x1=0，x2=3 | C、x1=-1，x2=1 | D、x1=-1，x2=3 |
已知二次函数y=-x2+bx+c的图象如图所示，它与x轴的一个交点坐标为（-1，0），与y轴的交点坐标为（0，3）．