题目内容
如图所示，在Rt△ABC中，CD是斜边AB上的高，求证：AC2∶BC2＝AD∶DB．
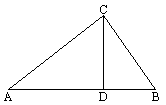
答案：
解析：
提示：
解析：
|
解答：因为CD是Rt△ABC斜边上的高，∴△ABC∽△CBD∽△ACD(直角三角形被斜边上的高分成的两个直角三角形和原三角形相似)． ∴ 同理可得：BC2＝AB·BD② ①式除以②式，得 分析：遇有比的问题，通常先证三角形相似，但AC2、BC2不是三角形一边，所以要将AC2、BC2用其他式子表示之后再求比． |
＝
，∴AC2＝AB·AD①
＝
＝
即AC2∶BC2＝AD∶DB．提示：
|
注意：①式、②式应用较多，最好掌握，会给今后的解题带来方便．但此结论不能直接用，要进行简单的推理． |
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
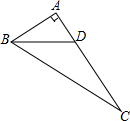如图所示，在Rt△ABC中，∠A=90°，BD平分∠ABC，交AC于点D，且AB=4，BD=5，则点D到BC的距离是（ ）
21、如图所示，在Rt△ABC中，∠ACB=90°，CD⊥AB，∠A=55°，则∠DCB=
22、如图所示，在Rt△ABC中，∠C=90°，∠A=30°．作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F，连接BE． 求证：EF=2DE．
如图所示，在Rt△ABC中，∠C=90°，AC=6，sinB=
如图所示，在Rt△ABC中，AD平分∠BAC，交BC于D，CH⊥AB于H，交AD于F，DE⊥AB垂足为E，求证：四边形CFED是菱形．