题目内容
 22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE.
22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE.分析:由∠C=90°,∠A=30°,根据三角形的内角和定理求出∠ABC的度数,由AB的中垂线,得到EA=EB,即求出∠2和∠1的度数,进一步求出∠F=30°,根据含30°的直角三角形的性质得到BE=2DE,根据等腰三角形的性质得到EF=BE,即可推出答案.
解答: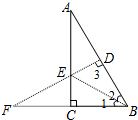 证明:如图,∵∠C=90°,∠A=30°,
证明:如图,∵∠C=90°,∠A=30°,
∴∠ABC=60°.
∵DF是AB的中垂线,
∴EA=EB,∠A=∠2=30°,
∴∠1=60°-∠2=30°,
∵∠3=90°,
∴∠F=90°-∠ABC=30°=∠1,
∴EF=BE=2DE,
即EF=2DE.
 证明:如图,∵∠C=90°,∠A=30°,
证明:如图,∵∠C=90°,∠A=30°,∴∠ABC=60°.
∵DF是AB的中垂线,
∴EA=EB,∠A=∠2=30°,
∴∠1=60°-∠2=30°,
∵∠3=90°,
∴∠F=90°-∠ABC=30°=∠1,
∴EF=BE=2DE,
即EF=2DE.
点评:本题主要考查了三角形的内角和定理,等腰三角形的性质,线段的垂直平分线定理.含30°角的直角三角形的性质等知识点,证BE=EF和求出∠2=30°是解此题的关键.题型较好.

练习册系列答案
相关题目
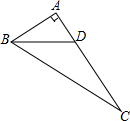 如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( ) 21、如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A=55°,则∠DCB=
21、如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A=55°,则∠DCB= 如图所示,在Rt△ABC中,∠C=90°,AC=6,sinB=
如图所示,在Rt△ABC中,∠C=90°,AC=6,sinB= 如图所示,在Rt△ABC中,AD平分∠BAC,交BC于D,CH⊥AB于H,交AD于F,DE⊥AB垂足为E,求证:四边形CFED是菱形.
如图所示,在Rt△ABC中,AD平分∠BAC,交BC于D,CH⊥AB于H,交AD于F,DE⊥AB垂足为E,求证:四边形CFED是菱形.