题目内容
 如图所示,在Rt△ABC中,AD平分∠BAC,交BC于D,CH⊥AB于H,交AD于F,DE⊥AB垂足为E,求证:四边形CFED是菱形.
如图所示,在Rt△ABC中,AD平分∠BAC,交BC于D,CH⊥AB于H,交AD于F,DE⊥AB垂足为E,求证:四边形CFED是菱形.分析:首先根据角平分线的性质以及垂直的定义得出∠3=∠4,即可得出FC=CD,进而得出FC∥DE,四边形CFED是平行四边形,进而得出答案.
解答: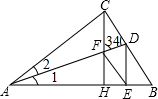 证明:∵AD平分∠BAC,
证明:∵AD平分∠BAC,
∴∠1=∠2,
∵在Rt△ABC中,CH⊥AB于H,
∴∠1+∠AFH=90°,∠2+∠4=90°,
∵∠3=∠AFH,∠1=∠2,
∴∠3=∠4,
∴FC=CD,
∵DE⊥AB垂足为E,∠ACD=90°,∠1=∠2,
∴CD=DE,∴FC=DE,
∵CH⊥AB,DE⊥AB,
∴FC∥DE,
∴四边形CFED是平行四边形,
∵FC=CD,
∴四边形CFED是菱形.
 证明:∵AD平分∠BAC,
证明:∵AD平分∠BAC,∴∠1=∠2,
∵在Rt△ABC中,CH⊥AB于H,
∴∠1+∠AFH=90°,∠2+∠4=90°,
∵∠3=∠AFH,∠1=∠2,
∴∠3=∠4,
∴FC=CD,
∵DE⊥AB垂足为E,∠ACD=90°,∠1=∠2,
∴CD=DE,∴FC=DE,
∵CH⊥AB,DE⊥AB,
∴FC∥DE,
∴四边形CFED是平行四边形,
∵FC=CD,
∴四边形CFED是菱形.
点评:此题主要考查了角平分线的性质以及平行线的判定和平行四边形的判定和菱形的判定,根据已知得出FC=CD是解题关键.

练习册系列答案
相关题目
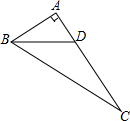 如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( ) 21、如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A=55°,则∠DCB=
21、如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A=55°,则∠DCB= 22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE.
22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE. 如图所示,在Rt△ABC中,∠C=90°,AC=6,sinB=
如图所示,在Rt△ABC中,∠C=90°,AC=6,sinB=