Question

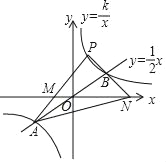
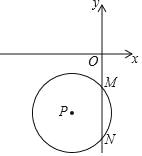
【题目】如图，半径为5的⊙P与y轴交于点M（0，﹣4），N（0，﹣10）

（1）求点P的坐标；

（2）将⊙P绕点O顺时针方向旋转90°后得⊙A，交x轴于B、C，求过A、B、C三个点的抛物线的解析式．

Answer 1

【答案】（1）点P的坐标为（﹣4，﹣7）；（2）y＝﹣x2﹣x﹣．

【解析】

（1）连接PM，PN，过点P作PE⊥y轴于点E，由点M，N的坐标可得出MN的长度，利用等腰三角形的三线合一可得出ME，OE的长度，在Rt△PEM中，利用勾股定理可得出PE的长度，结合OE的长度及点P所在的象限即可得出点P的坐标；

（2）连接OP，OA，AB，AC（设点B在点C的右边），过点P作PE⊥y轴于点E，过点A作AF⊥x轴于点F，根据旋转的性质可得出点A的坐标，在Rt△AFB中，利用勾股定理可得出BF的长度，进而可得出OB，OC的长，由OB，OC在x轴负半轴可得出点B，C的坐标，再由点A，B，C的坐标，利用待定系数法可求出过A，B，C三个点的抛物线的解析式．

（1）连接PM，PN，过点P作PE⊥y轴于点E，如图1所示．

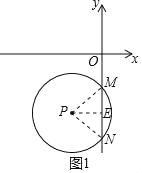
∵PM＝PN，

∴ME＝NE．

∵点M（0，﹣4），N（0，﹣10），

∴OM＝4，MN＝﹣4﹣（﹣10）＝6，ME＝MN＝3，

∴OE＝OM+ME＝7．

在Rt△PEM中，∠PEM＝90°，PM＝5，ME＝3，

∴PE＝＝4，

∴点P的坐标为（﹣4，﹣7）．

（2）连接OP，OA，AB，AC（设点B在点C的右边），过点P作PE⊥y轴于点E，过点A作AF⊥x轴于点F，如图2所示．

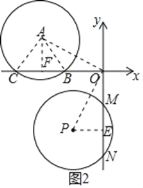
根据旋转的性质，可知：OD＝OE＝7，AF＝PE＝4，

∴点A的坐标为（﹣7，4）．

在Rt△AFB中，∠AFB＝90°，AF＝4，AB＝5，

∴BF＝＝3，

∴OB＝OF﹣BF＝4．

同理：CF＝3，OC＝OF+CF＝10，

∴点B的坐标为（﹣4，0），点C的坐标为（﹣10，0）．

设过A，B，C三个点的抛物线的解析式为y＝ax2+bx+c（a≠0），

将A（﹣7，4），B（﹣4，0），C（﹣10，0）代入y＝ax2+bx+c，得：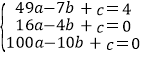

解得：，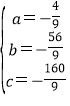

∴过A，B，C三个点的抛物线的解析式为y=-x2-x-．