题目内容
【题目】已知二次函数y=x2+bx+c(其中b,c为常数,c>0)的顶点恰为函数y=2x和y=![]() 的其中一个交点.则当a2+ab+c>2a>
的其中一个交点.则当a2+ab+c>2a>![]() 时,a的取值范围是
时,a的取值范围是
【答案】-1<a<0或a>3
【解析】
先求出抛物线的顶点坐标,再求出抛物线与直线y=2x的交点,然后结合函数图象就可解决问题.
解方程组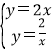 得:
得:![]() ,
,![]() .
.
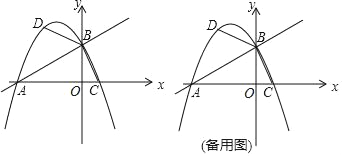
①当抛物线y=x2+bx+c顶点为(1,2)时,
抛物线的解析式为y=(x-1)2+2=x2-2x+3.
解方程组![]() 得:
得:![]() ,
,![]() .
.
结合图象可得: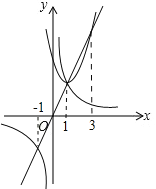
当a2+ab+c>2a>![]() 时,a的取值范围是-1<a<0或a>3;
时,a的取值范围是-1<a<0或a>3;
②当抛物线y=x2+bx+c顶点为(-1,-2)时,
抛物线的解析式为y=(x+1)2-2=x2+2x-1.
∴c=-1<0,与条件c>0矛盾,故舍去.
故答案是:-1<a<0或a>3.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目