Question

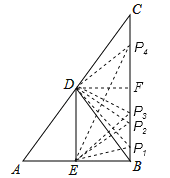
【题目】如图，在Rt△ABC中，∠ABC=90°，点D是AC的中点，作∠ADB的角平分线DE交AB于点E，

（1）求证：DE∥BC；

（2）若AE=3，AD=5，点P为线段BC上的一动点，当BP为何值时，△DEP为等腰三角形．请求出所有BP的值．

Answer 1

【答案】（1）证明见解析（2），2，4﹣，4+．

【解析】试题分析：（1）根据直角三角形斜边上的中线等于斜边的一半可得BD=AD=AC，再根据等腰三角形三线合一的性质可得DE⊥AB，再根据垂直于同一直线的两直线平行证明；

（2）利用勾股定理列式求出DE的长，根据等腰三角形三线合一的性质求出BE=AE，然后分DE=EP、DP=EP、DE=DP三种情况讨论求解．

试题解析：（1）证明：∵∠ABC=90°，点D是AC的中点，∴BD=AD=AC，∵DE是∠ADB的角平分线，∴DE⊥AB，又∵∠ABC=90°，∴DE∥BC；

（2）解：∵AE=3，AD=5，DE⊥AB，∴DE= =4，∵DE⊥AB，AD=BD，∴BE=AE=3．

①DE=EP时，BP==；

②DP=EP时，BP=DE=×4=2；

③DE=DP时，过点D作DF⊥BC于F，则DF=BE=3，由勾股定理得，FP==，点P在F下边时，BP=4﹣，点P在F上边时，BP=4+．

综上所述，BP的值为，2，4﹣，4+．