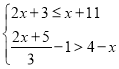题目内容
【题目】电影“阿凡达”自上映以来取得了空前的票房收入,某小区居民决定通过居委会向影院购买一些3D票供每户家庭观看,最终购得成人票数量是学生(孩子)票数量的3倍,购买的总费 用不低干2200元,但不高于2500元
(1)电影院成人票售价20元/人,学生票售价为50元/人,问:有哪几种购买方案?
(2)在(1)的方案中,哪一种方案的总费用最少?最少费用是多少元?
(3)由于当天电影院同时播放“拆弹部队”,故决定成人票打九折,学生票打八折,用(2)中的最少费用最多还可以多买多少张成人票和学生票?
【答案】(1)见解析;(2)220;(3)多买9张成人票和3张儿童票.
【解析】(1)设成人人数为x,则儿童人数为![]() x,由“成人票售价20元/人,学生票售价为50元/人”和“总费用不低干2200元,但不高于2500元”得不等式组求解即得;
x,由“成人票售价20元/人,学生票售价为50元/人”和“总费用不低干2200元,但不高于2500元”得不等式组求解即得;
(2)计算出(1)中各种方案需要的钱就知道哪一种方案的总费用最少,最少费用是多少元;
(3)计算出最少费用通过打折后多余的钱算出能买成人和儿童的票数.
(1)设成人人数为x,则儿童人数为![]() x,根据题意得
x,根据题意得
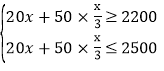 ,
,
解得:![]() ,
,
∵x为正整数∴x可取60,61,62,63,64,65,66,67,68,
∵![]() 也必需是整数,∴x可取60,63,66,
也必需是整数,∴x可取60,63,66,
∴有三种购买方案:
方案一:成人票60张,儿童票20张:
方案二:成人票63张,儿童票21张:
方案一:成人票66张,儿童票22张:
(2)在(1)中,
方案一购买票的总数量为:80,总费用为:60×20+20×50=2200,
方案一购买票的总数量为:84,总费用为:63×20+21×50=2310,
方案一购买票的总数量为:80,总费用为:66×20+22×50=2420.
故第一种方案的总费用最少,最少费用是2200元;
(3)设用(2)中的最少费用还可以多买儿童票数量为y,
![]() ,
,
解得:![]() ,
,
∵y为正整数,
∴满足![]() 的最大正整数为3,
的最大正整数为3,
∴多买的成人票为:![]() (张),
(张),
答:用(2)中的最少费用最多还可以多买9张成人票和3张儿童票.

 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案