��Ŀ����
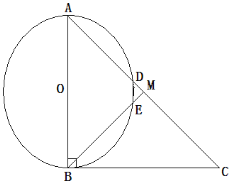
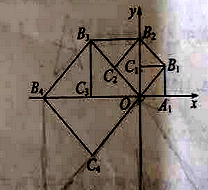
����Ŀ����ͼ1��������OABC�ı�OA�������ϣ�OΪԭ�㣬������OABC�����Ϊ12��OC�߳�Ϊ3.

(1)�����ϵ�A��ʾ����Ϊ________��
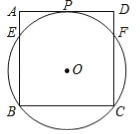
(2)��������OABC������ˮƽ�ƶ����ƶ���ij����μ�ΪO��A��B��C�����ƶ���ij�����O��A��B��C����ԭ������OABC�ص�����(��ͼ2����Ӱ����)�������ΪS.
�ٵ�Sǡ�õ���ԭ������OABC�����һ��ʱ�������ϵ�A����ʾ�����Ƕ��٣�
�� �����A���ƶ�����AA����x.
�� ����)��S��4ʱ����x��ֵ��
�� ����)DΪ�߶�AA�����е㣬��E���߶�OO���ϣ���OE��![]() OO��������D��E����ʾ������Ϊ�෴��ʱ����x��ֵ��
OO��������D��E����ʾ������Ϊ�෴��ʱ����x��ֵ��
���𰸡�4
����������1���������+OC�ɵ�AO�������ɵô𰸣�
��2�������ȼ����S��ֵ���ٸ��ݾ��ε������ʾ��O/A�ij��ȣ��ٷ�����������������˶�ʱ�������˶�ʱ���ֱ����A/��ʾ������
��i�����ȸ�������ɵ�OA/�ij��ȣ�����OA����ȥOA/���ɵ�x��ֵ��
Ii������������������ԭ������OABC�����ƶ�ʱ����D��ʾ����Ϊ4 -![]() x����E��ʾ����Ϊ-
x����E��ʾ����Ϊ-![]() x��ԭ������OABC�����ƶ�ʱ����D��E��ʾ������������������������.
x��ԭ������OABC�����ƶ�ʱ����D��E��ʾ������������������������.
�⣺��1���߳�����OABC�����Ϊ12��OC�߳�Ϊ3��
��OA=12��3=4��
�������ϵ�A��ʾ����Ϊ4.
�ʴ�Ϊ��4.
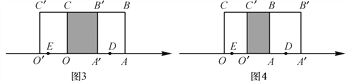
(2)����ΪSǡ�õ���ԭ������OABC�����һ�룬����S��6������O��A��6��3��2����������OABC�����˶�ʱ����ͼ3��A����ʾ����Ϊ2����������OABC�����˶�ʱ����ͼ4����ΪO��A����AO��4������OA����4��4��2��6������A����ʾ����Ϊ6.�������ϵ�A����ʾ������6��2.
 ��
��
�ڣ�i)��ͼ3���������CO��OA����4����ΪCO��3������OA����![]() ������x��4��
������x��4��![]() ��
��![]()
��ii)��ͼ3����ԭ������OABC�����ƶ�ʱ����D��ʾ����Ϊ4��![]() x����E��ʾ����Ϊ��
x����E��ʾ����Ϊ��![]() x��������ɵ÷��̣�4��
x��������ɵ÷��̣�4��![]() x��
x��![]() x��0�����x��
x��0�����x��![]() ����ͼ4����ԭ������OABC�����ƶ�ʱ����D��E��ʾ�����������������������⣬����ȥ��������������x��
����ͼ4����ԭ������OABC�����ƶ�ʱ����D��E��ʾ�����������������������⣬����ȥ��������������x��![]() .
.
���㾦��������Ҫ������һԪһ�η��̵�Ӧ�ã����ᣬ����ؼ�����ȷ�������⣬�������ν���г����̣�ע��Ҫ�������ۣ���Ҫ©��.

 ��ʦ�㲦��ϵ�д�
��ʦ�㲦��ϵ�д� Ӣ�żƻ���ĩ����ϵ�д�
Ӣ�żƻ���ĩ����ϵ�д�