题目内容
【题目】在平面直角坐标系xOy中的点P(x,y)(x≠0),将它的纵坐标y与横坐标x的比称为点P的“湘一比”,记为kp,如点P(﹣3,6),则kp=![]() =﹣2.
=﹣2.
(1)若P(a,2)在直线y=x﹣2上,求点P的“湘一比”kp及直线OP与x轴夹角的正切值;
(2)已知点Q(m,n)的“湘一比”kQ为![]() ,且Q在y=
,且Q在y=![]() (x>0)上,⊙Q的半径为1,若点M在⊙Q上,求M的“湘一比”kM的取值范围;
(x>0)上,⊙Q的半径为1,若点M在⊙Q上,求M的“湘一比”kM的取值范围;
(3)设m、n为正整数,且m≠2,对一切实数t,如果直线y=mtx+3mt与二次函数y=x2+3x交于A(x1,y1),B(x2,y2),且|x1﹣x2|≥|2t+n|,求点N(m,n)的“湘一比”kN的值.
【答案】(1)kp=![]() ,直线OP与x轴夹角的正切值是
,直线OP与x轴夹角的正切值是![]() ;(2)0≤kM≤
;(2)0≤kM≤![]() ;(3)kN=
;(3)kN=![]() 或
或![]() .
.
【解析】
(1)根据一次函数图象上点的坐标特征求出a的值,再根据 “湘一比”的定义求出kp,然后作出图形,利用正切的定义求直线OP与x轴夹角的正切值;
(2)先确定出点Q的坐标,进而判断出直线OM和⊙Q相切时是分界点,分别求出相切时kM的最大值和最小值,即可得出结论;
(3)联立解析式,求出x1=3,x2=mt,进而建立不等式组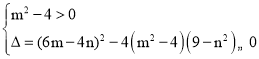 ,得出m>2且(mn6)2≤0,进而确定出m,n的值,即可得出结论.
,得出m>2且(mn6)2≤0,进而确定出m,n的值,即可得出结论.
解:(1)∵P(a,2)在直线y=x﹣2上,
∴2=a﹣2,
∴a=4,
∴kp=![]() =
=![]() ,
,
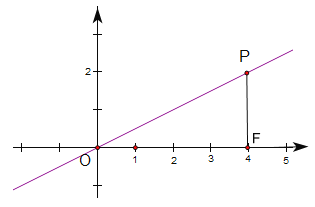
如图,过点P作PF⊥x轴于F,
∵P(4,2),
∴PF=2,OF=4,
∴此时直线OP与x轴夹角的正切值为:![]() ;
;
(2)由题意知,kQ=![]() =
=![]() ,
,
∴n=![]() m,
m,
∴Q(m,![]() m),
m),
∵Q在y=![]() (x>0)上,
(x>0)上,
∴![]() ,
,
∴![]() 或m=﹣
或m=﹣![]() (舍去),
(舍去),
∴![]()
根据点M的“湘一比”知,直线OM和⊙Q相切时,一个是kM的最大值,一个是kM的最小值,
∵![]() ,⊙Q的半径为1,
,⊙Q的半径为1,
∴⊙Q与x轴相切,
如图,切点为M1(![]() ,0),故此时kM最小,即kM=0;
,0),故此时kM最小,即kM=0;
而直线OM2是⊙Q的另一条切线,此时kM最大,
∵![]() ,
,
∴![]() ,
,
∵OM1,OM2分别为⊙Q的两条切线,
∴OM1=OM2=![]() ,
,![]() ,
,
∴![]() ,
,
过点M2作M2E⊥x轴于点E,则OE=![]() ,
,![]() ,
,
∴当点M2坐标为(![]() ,
,![]() )时,kM最大,此时kM=
)时,kM最大,此时kM=![]() ,
,
∴0≤kM≤![]() ;
;

(3)联立![]() ,
,
∴x2+(3﹣mt)x﹣3mt=0,即(x+3)(x-mt)=0,
∴x1=﹣3,x2=mt,
∵|x1﹣x2|≥|2t+n|,
∴(﹣3﹣mt)2≥(2t+n)2,整理得:![]() ,
,
由题意知,对于一切实数t不等式恒成立,∴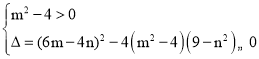 ,
,
∵m为正整数,
∴m>2且(mn﹣6)2≤0,
∵(mn﹣6)2≥0,
∴mn=6,
∵m,n为正整数,
∴m=3,n=2或m=6,n=1,
∴kN=![]() 或
或![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0;
②当x>1时,y的值随x值的增大而减小.
③3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
其中正确的结论是 .