题目内容
已知:如图,⊙O与⊙P相交于A、B两点,点P在⊙O上,⊙O的弦AC切⊙P于点A,CP及其 延长线交⊙P于D、E,过点E作EF⊥CE交CB的延长线于F.
延长线交⊙P于D、E,过点E作EF⊥CE交CB的延长线于F.(1)求证:BC是⊙P的切线;
(2)若CD=2,CB=2
| 2 |
(3)若设PE:CE=k,是否存在实数k,使△PBD恰好是等边三角形?若存在,求出k的值;若不存在,请说明理由.
分析:(1)要证明BC是⊙P的切线,则连接BP,需要证明BP⊥BC.根据已知条件,连接AP.根据切线的性质得到∠PAC=90°,再根据圆周角定理的推论得到CP是直径,从而得到∠CBP=90°,证明结论;
(2)首先根据切割线定理求得CE的长,再根据勾股定理和切线长定理求得EF的长;
(3)根据等边三角形的性质和30度的直角三角形的性质进行求解.
(2)首先根据切割线定理求得CE的长,再根据勾股定理和切线长定理求得EF的长;
(3)根据等边三角形的性质和30度的直角三角形的性质进行求解.
解答: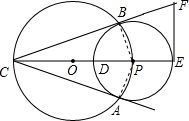 (1)证明:连接PA、PB;
(1)证明:连接PA、PB;
∵AC切⊙P于A,PA是⊙P的半径,
∴AC⊥PA.
即:∠PAC=90°,
即PB⊥CB.
又∵PB是⊙P的半径,
∴BC是⊙P的切线.
(2)解:由切割线定理得:BC2=CD•CE,
∴CE=
=
=4.
设EF=x,
根据勾股定理,得x2=(x+2
)2-16
∴x=
.
(3)解:∵△PBD为等边三角形,
∴∠CPB=60°.
∵CB是⊙P的切线,
∴CB⊥BP,
∴∠BCP=30°,△PBC为Rt△,
∴PB=
PC,PB=PE;
∴PC=2PE,CE=PC+PE,
∴CE=3PE,
∴PE:CE=
.
即:k=
时,△PBD为等边三角形.
 (1)证明:连接PA、PB;
(1)证明:连接PA、PB;∵AC切⊙P于A,PA是⊙P的半径,
∴AC⊥PA.
即:∠PAC=90°,
即PB⊥CB.
又∵PB是⊙P的半径,
∴BC是⊙P的切线.
(2)解:由切割线定理得:BC2=CD•CE,
∴CE=
| BC2 |
| CD |
(2
| ||
| 2 |
设EF=x,
根据勾股定理,得x2=(x+2
| 2 |
∴x=
| 2 |
(3)解:∵△PBD为等边三角形,
∴∠CPB=60°.
∵CB是⊙P的切线,
∴CB⊥BP,
∴∠BCP=30°,△PBC为Rt△,
∴PB=
| 1 |
| 2 |
∴PC=2PE,CE=PC+PE,
∴CE=3PE,
∴PE:CE=
| 1 |
| 3 |
即:k=
| 1 |
| 3 |
点评:掌握切线的判定方法和性质,能够熟练运用切割线定理、勾股定理以及特殊三角形的性质.

练习册系列答案
相关题目
 21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.
21、已知:如图,⊙O1与⊙O2相交于A、B两点,过A的直线交⊙O1于C,交⊙O2于D,过B的直线交⊙O1于E,交⊙O2于F,且CD∥EF.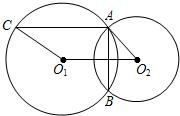 ,⊙O2的半径为
,⊙O2的半径为 14、已知:如图,⊙O1与⊙O2外切于点P,⊙O1的半径为3,且O1O2=8,则⊙O2的半径R=
14、已知:如图,⊙O1与⊙O2外切于点P,⊙O1的半径为3,且O1O2=8,则⊙O2的半径R= (1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D.
(1997•南京)已知:如图,⊙O1与⊙O2外切于点P,A为⊙O1上一点,直线AC切⊙O2于点C,且交⊙O1于点B,AP的延长线交⊙O2于点D. 已知:如图,⊙O1与⊙O2相交于A,B两点.求证:直线O1O2垂直平分AB.
已知:如图,⊙O1与⊙O2相交于A,B两点.求证:直线O1O2垂直平分AB.