题目内容
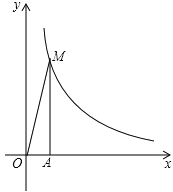
【题目】(10分)某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示.

(l)甲厂的制版费为____千元,印刷费为平均每个 元,甲厂的费用yl与证书数量x之间的函数关系式为 ,
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个 元;
(3)当印制证书数量超过2干个时,求乙厂的总费用y2与证书数量x之间的函数关系[式;
(4)若该单位需印制证书数量为8干个,该单位应选择哪个厂更节省费用?请说明理由.
【答案】(1)1;0.5;y=0.5x+1;
(2)1.5;
(3)![]() ;
;
(4)由图象可知,当x=8时,y1>y2,因此该单位选择乙厂更节省费用.
【解析】
试题分析:(1)由图得制版费是1千元,通过坐标(0,1)(2,2)求出函数解析式,印刷单价=(印刷费用-制版费)÷2000;
(2)由图像可知,用3千元÷2千个,即可得到乙厂的平均印刷费;
(3)设y2=kx+b,由图可知,当x=6时y1与y2相交,利用(1)中求出的函数关系式可求出相应的值,把这一点和(2,3)点代入设的解析式,即可求出相应的函数关系式;
(4) 分别求出甲乙两车的费用y关于证书个数x的函数,将x=8分别代入两个函数求值比较即可,可得出选择乙厂节省.
试题解析:(10分)
(1)1;0.5;y=0.5x+1;
(2)1.5;
(3)设y2=kx+b,
由图可知,当x=6时,y2=y1=0.5×6+1=4,
所以函数图象经过点(2,3)和(6,4).
所以把(2,3)和(6,4)代入y2=kx+b,得![]() ,
,
解得![]() ,所以y2与x之间的函数关系式为
,所以y2与x之间的函数关系式为![]() .
.
(4)由图象可知,当x=8时,y1>y2,因此该单位选择乙厂更节省费用.
(求出当x=8时,y1和y2的值,用比较大小的方法得到结论也正确)

【题目】下表所示为装运、销售甲、乙、丙三种蔬菜的重量及利润。某公司计划用20辆汽车装运甲、乙、丙三种蔬菜共36吨到某地销售.规定每辆汽车满载,每车只装一种蔬菜,每种蔬菜不少于一车。应如何安排,可使公司获得利润18300元?
甲 | 乙 | 丙 | |
每辆汽车装运的吨数 | 2 | 1 | 1.5 |
每吨蔬菜可获利润(百元) | 5 | 7 | 4 |