题目内容
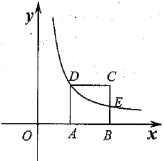
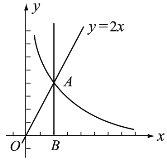
【题目】如图,曲线l是由函数y=![]() 在第一象限内的图象绕坐标原点O逆时针旋转90°得到的,且过点A (m,6),B (﹣6,n),则△OAB的面积为_____.
在第一象限内的图象绕坐标原点O逆时针旋转90°得到的,且过点A (m,6),B (﹣6,n),则△OAB的面积为_____.
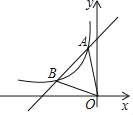
【答案】16
【解析】
作AM⊥y轴于M,BN⊥x轴于N,直线AM与BN交于点P,根据旋转的性质得出点A(m,6),B(-6,n)在函数y=-![]() 的图象上,根据待定系数法求得m、n的值,继而得出P(6,6),然后根据S△AOB=S矩形OMPN-S△OAM-S△OBN-S△PAB即可求得结果.
的图象上,根据待定系数法求得m、n的值,继而得出P(6,6),然后根据S△AOB=S矩形OMPN-S△OAM-S△OBN-S△PAB即可求得结果.
解: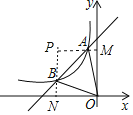
作AM⊥y轴于M,BN⊥x轴于N,直线AM与BN交于点P,
∵曲线l是由函数y=![]()
在第一象限内的图象绕坐标原点O逆时针旋转90°得到的,且过点A(m,6),B(-6,n),
∴点A(m,6),B(-6,n)在函数y=-![]() 的图象上,
的图象上,
∴6m=-12,-6n=-12,
解得m=-2,n=2,
∴A(-2,6),B(-6,2),
∴P(-6,6),
∴S△AOB=S矩形OMPN-S△OAM-S△OBN-S△PAB=6×6-![]() ×2×6-
×2×6-![]() ×6×2-
×6×2-![]() ×4×4=16,
×4×4=16,
故答案为16.

练习册系列答案
相关题目