题目内容
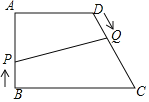
【题目】已知:如图,在四边形ABCD中,AD∥BC,∠A=90°,AB=AD=8cm,CD=10cm,点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为lcm/s.连接PQ,设运动时间为t(s)(0<t<8).解答下列问题:
(1)当t为何值时,PQ∥AD?
(2)设四边形APQD的面积为y(cm2),求y与t的函数关系式;
(3)是否存在某一时刻t,使S四边形APQO:S四边形BCQP=17:27?若存在,求出t的值,并求此时PQ的长;若不存在,请说明理由.
【答案】(1)当t为![]() s时,PQ∥AD;(2)y与t的函数关系式是y=
s时,PQ∥AD;(2)y与t的函数关系式是y=![]() ;(3)t的值为2s或
;(3)t的值为2s或![]() s,此时PQ的长为
s,此时PQ的长为![]() cm,见解析.
cm,见解析.
【解析】
(1)根据平行线分线段成比例的性质解答即可;
(2)过点D作DE⊥BC于点E,过点Q作QF⊥AD交AD的延长线于F,根据矩形的性质和三角函数解答即可;
(3)过点Q作QH⊥AB于点H,根据四边形面积公式进行解答即可.
解:(1)∵PQ∥AD,AD∥BC
∴![]() ,
,
即![]()
解得,![]()
答:当t为![]() s时,PQ∥AD.
s时,PQ∥AD.
(2)过点D作DE⊥BC于点E,过点Q作QF⊥AD交AD的延长线于F
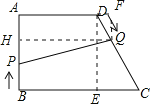
∴∠DEC=∠QFD=90°
∵AD∥BC,∠A=90°
∴∠ABC=180°-∠A=90°
∴四边形ABND是矩形
∴AB=DE,BE=AD
在Rt△DEC中,![]() ,
,
∵∠C=∠QDF
∴在Rt△DFQ和Rt△DEC中,
sin∠QDF=![]() ,即
,即![]()
∴![]()
cos∠QDF=![]() ,即
,即![]()
∴![]()
∵在四边形ABCD中,∠A=90°,AB=AD
∴∠ABD=∠ADB=45°
∴y=S四边形APQD=S四边形APQF-S△DQF
=![]()
=![]()
=![]()
答:y与t的函数关系式是y=![]() .
.
(3)若S四边形APQD:S四边形BCQP=17:27,则y=![]() S四边形ABCD
S四边形ABCD
∵S四边形ABCD=![]()
∴![]() =34
=34
解得t1=2,![]()
∴t的值为2s或![]() s.
s.
过点Q作QH⊥AB于点H,
∴PH=![]()
QH=AF=![]()
∴PQ=![]()
当t=2时,PQ=![]()
当t=![]() 时,PQ=
时,PQ=![]()
∴此时PQ的长为![]() cm.
cm.