��Ŀ����
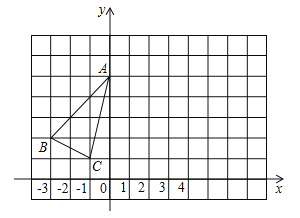
����Ŀ������y=x2+bx+c��ͼ����x �ύ��A��B���㣬��y�ύ�ڵ�C��OB=OC����D�ں���ͼ���ϣ�CD//x�ᣬ��CD=2��ֱ��l �������ߵĶԳ��ᣬE�������ߵĶ��㣮
��1����b��c ��ֵ��
��2����ͼ��������BE���߶�OC �ϵĵ�F ����ֱ��l �ĶԳƵ�F�� ǡ�����߶�BE�ϣ����F�����ꣻ
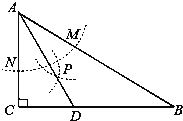
��3����ͼ��������P���߶�OB�ϣ�����P ��x ��Ĵ��߷ֱ���BC���ڵ�M���������߽��ڵ�N�����ʣ����������Ƿ���ڵ�Q��ʹ����PQN����APM�������ȣ����߶�NQ�ij�����С��������ڣ������Q�����ꣻ��������ڣ�˵�����ɣ�

ͼ �� ͼ��
���𰸡���1��c=-3����2����F������Ϊ��0��-2������3����������ĵ�Q������Ϊ��![]() ,
,![]() ����(
����(![]() ,
,![]() )
)
��������
��1������������������߶Գ�����������b��ֵ����OB=OC������c��ʾ��B�����������������߽���ʽ�����c��ֵ��
��2������F��0��m������ɱ�ʾ��F������������B��E����������ֱ��BE�Ľ���ʽ����F���������ֱ��BE����ʽ�ɵõ�����m�ķ����������F���������
��3�����P����Ϊ��n��0�����ɱ�ʾ��PA��PB��PN�ij�����QR��PN������ΪR��������QR�ij�����n�ɱ�ʾ��Q��R��N�����꣮��Rt��QRN�����ɹ��ɶ����ɵõ�����n�Ķ��κ��������ö��κ��������ʿ�֪��ȡ����Сֵʱn��ֵ��������Q���������
��1����CD��x����CD=2���������߶Գ���Ϊx=1����![]() ��
��
��OB=OC��C��0��c������B�������Ϊ����c��0������0=c2+2c+c�������c=��3��c=0����ȥ������c=��3��
��2�����F��������0��m����
�߶Գ���Ϊֱ��x=1�����F����ֱ��l�ĶԳƵ�F������Ϊ��2��m����
�ɣ�1����֪�����߽���ʽΪy=x2��2x��3=��x��1��2��4����E��1����4����
��ֱ��BE������B��3��0����E��1����4���������ô���ϵ�����ɵ�ֱ��BE�ı���ʽΪy=2x��6��
�ߵ�F��BE������m=2��2��6=��2������F������Ϊ��0����2����
��3�����ڵ�Q����������
���P������n��0������PA=n+1��PB=PM=3��n��PN=��n2+2n+3��
��QR��PN������ΪR��
��S��PQN=S��APM����![]() ����QR=1��
����QR=1��
������������ۣ�
�ٵ�Q��ֱ��PN�����ʱ��Q�������Ϊ��n��1��n2��4n����R�������Ϊ��n��n2��4n����N�������Ϊ��n��n2��2n��3��������Rt��QRN����NQ2=1+��2n��3��2����![]() ʱ��NQȡ��Сֵ1����ʱQ�������Ϊ
ʱ��NQȡ��Сֵ1����ʱQ�������Ϊ![]() ��
��
�ڵ�Q��ֱ��PN���Ҳ�ʱ��Q�������Ϊ��n+1��n2��4����
ͬ����NQ2=1+��2n��1��2����![]() ʱ��NQȡ��Сֵ1����ʱQ�������Ϊ
ʱ��NQȡ��Сֵ1����ʱQ�������Ϊ![]() ��
��
���Ͽ�֪������������ĵ�Q��������Ϊ![]() ��
��![]() ��
��