题目内容
【题目】如图,A、B两点的坐标分别为(0,6),(0,3),点P为x轴正半轴上一动点,过点A作AP的垂线,过点B作BP的垂线,两垂线交于点Q,连接PQ,M为线段PQ的中点.

(1)求证:A、B、P、Q四点在以M为圆心的同一个圆上;
(2)当⊙M与x轴相切时,求点Q的坐标;
(3)当点P从点(2,0)运动到点(3,0)时,请直接写出线段QM扫过图形的面积.
【答案】(1)见解析;(2) Q的坐标为(3![]() ,9);(3)
,9);(3)![]() .
.
【解析】(1)解:连接AM、BM,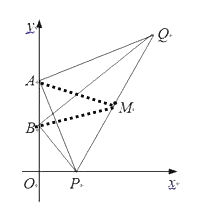
∵AQ⊥AP,BQ⊥BP∵△APQ和△BPQ都是直角三角形,M是斜边PQ的中点
∴AM=BM=PM=QM= ![]() PQ,
PQ,
∴A、B、P、Q四点在以M为圆心的同一个圆上。
(2)解:作MG⊥y轴于G,MC⊥x轴于C,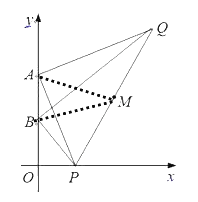
∵AM=BM
∴G是AB的中点,由A(0,6),B(0,3)可得MC=OG=4.5
∴在点P运动的过程中,点M到x轴的距离始终为4.5
则点Q到x轴的距离始终为9,即点Q的纵坐标始终为9,
当⊙M与x轴相切时则PQ⊥x轴,作QH⊥y轴于H,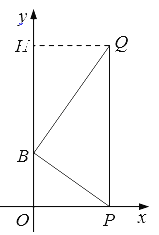
HB=9-3=6,设OP=HQ=x
由△BOP∽△QHB,得x2=3×6=8,x=3 ![]()
∴点Q的坐标为(3![]() ,9)
,9)
(3)解:由相似可得:当点P在P1(2,0)时,Q1(4,9)则M1(3,4.5)
当点P在P2(3,0)时,Q2(6,9),则M2(4.5,4.5)
∴M1M2= ![]() -3=
-3= ![]() , Q1Q2=6-4=2
, Q1Q2=6-4=2
线段QM扫过的图形为梯形M1M2Q2Q1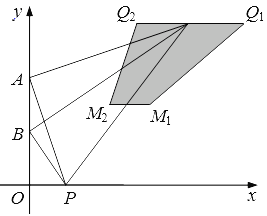
其面积为:![]() ×(
×(![]() +2)×4.5=
+2)×4.5=![]() .
.
【解析】
根据已知可得出三角形APQ和三角形BPQ都是直角三角形,再根据这个条件结合题意直接解答此题.
(1)解:连接AM、BM,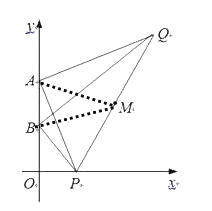
∵AQ⊥AP,BQ⊥BP∵△APQ和△BPQ都是直角三角形,M是斜边PQ的中点
∴AM=BM=PM=QM= ![]() PQ,
PQ,
∴A、B、P、Q四点在以M为圆心的同一个圆上。
(2)解:作MG⊥y轴于G,MC⊥x轴于C,
∵AM=BM
∴G是AB的中点,由A(0,6),B(0,3)可得MC=OG=4.5
∴在点P运动的过程中,点M到x轴的距离始终为4.5
则点Q到x轴的距离始终为9,即点Q的纵坐标始终为9,
当⊙M与x轴相切时则PQ⊥x轴,作QH⊥y轴于H,
HB=9-3=6,设OP=HQ=x
由△BOP∽△QHB,得x2=3×6=8,x=3 ![]()
∴点Q的坐标为(3 ![]() ,9)
,9)
(3)解:由相似可得:当点P在P1(2,0)时,Q1(4,9)则M1(3,4.5)
当点P在P2(3,0)时,Q2(6,9),则M2(4.5,4.5)
∴M1M2= ![]() -3=
-3= ![]() , Q1Q2=6-4=2
, Q1Q2=6-4=2
线段QM扫过的图形为梯形M1M2Q2Q1
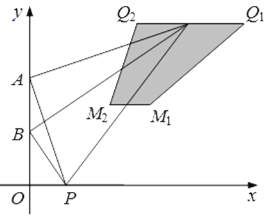
其面积为:![]() ×(
×( ![]() +2)×4.5=
+2)×4.5=![]() .
.